参考:http://www.dyn4j.org/2010/04/gjk-gilbert-johnson-keerthi/
和SAT(分离轴)法一样, GJK可以判断两个凸图形是否重叠. 比起SAT, GJK优在用同一套办法可以处理所有的图形, 而SAT判断某两种不同图形(多边形-多边形/多边形-圆形/圆形-圆形等)都要区别处理.
GJK原理: 如果两个凸图形的闵可夫斯基差包含原点, 那么这两个图形重叠. 所以问题转变成判断一个闵可夫斯基差图形是否包含原点.
闵可夫斯基和就是把两个图形里的点都当作向量, 把两个图形里的向量点都分别相加, 得到一个新的图形.
闵可夫斯基差就是把其中一个图形的向量都取反, 相当于绕原点反转, 然后再把两个图形求闵可夫斯基和.
GJK不会直接求两个图形的闵可夫斯基差, 而是通过下面这个辅助函数, 输入不同的查找方向, 返回闵可夫斯基差上的一个点, 迭代地用这些点组成一个个子图形, 判断子图形是否包含原点.
proc getSupportPoint(s1: Sprite2D, s2: Sprite2D, dir: Vector2D): Vector2D =
let
invM1 = s1.invMatrix
invM2 = s2.invMatrix
v1 = s1.matrix * s1.graph.getFarthestPointInDirection(invM1 * dir - invM1 * Vector2D(x: 0, y: 0))
v2 = s2.matrix * s2.graph.getFarthestPointInDirection(invM2 * dir.negate() - invM2 * Vector2D(x: 0, y: 0))
return v1 - v2
上面这个函数会返回闵可夫斯基差图形在某个方向上最远的一个点. 这里先把查找方向变换到物体空间, 由物体自己找到自身在查找方向上的最远点后, 再变换回世界空间.
查找多边形在查找方向上的最远的点的函数如下. 通过把所有顶点投影到查找方向上, 根据投影的大小判断距离.
method getFarthestPointInDirection*(self: Polygon, direction: Vector2D): Vector2D =
var
curr = self[0]
bestProjection: float32 = curr * direction
projection: float32
result = curr
for i in 1..self.len-1:
curr = self[i]
projection = curr * direction
if projection > bestProjection:
bestProjection = projection
result = curr
圆形. norm是求单位向量.
method getFarthestPointInDirection*(self: Circle, direction: Vector2D): Vector2D =
direction.norm() * self.radius
GJK每次生成的子图形都是单纯形(simplex). 单纯形在2D下是三角形, 在3D下是四面体.
维基上给出的GJK伪代码如下:
function GJK_intersection(shape p, shape q, vector initial_axis):
vector A = Support(p, initial_axis) - Support(q, -initial_axis)
simplex s = {A}
vector D = -A
loop:
A = Support(p, D) - Support(q, -D)
if dot(A, D) < 0:
reject
s = s ∪ A
s, D, contains_origin = NearestSimplex(s)
if contains_origin:
accept
个人的具体实现如下:
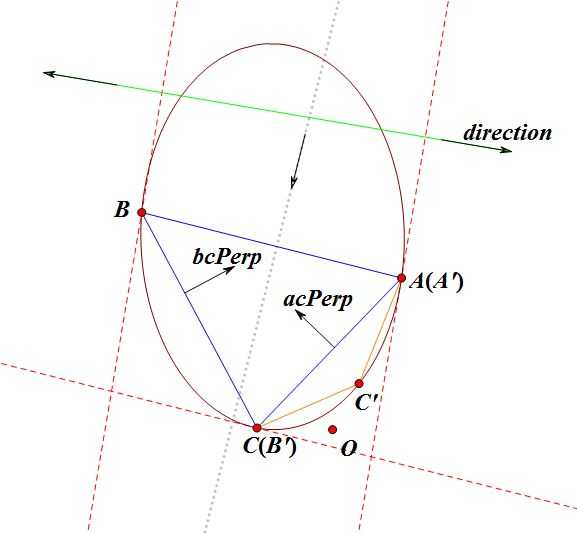
假设闵可夫斯基差的图形是下图的椭圆形.
首先随便用一个初始查找方向, 通过getSupportPoint函数找到单纯形上的第一个点A. 此时, 把向量OA投影到查找方向向量上. 如果投影是负数, 那么原点O一定在闵可夫斯基差外(在下图是过A的红色虚线右侧), 判定为两图形不重叠. 之后每次找到一个单纯形的顶点都如此判断.
然后, 把查找方向取反(或者用AO方向也可), 找到第二个点B. 然后判断原点不在过点B的虚线左侧.
把A和B连线, 求指向AO方向的垂直于AB的一个向量当作查找方向, 得到点C. 现在, 原点可能存在的地方就是三条红色虚线与AB包围的四边形内了.
求垂直于AC的指向AB方向的向量acPerp, 求垂直于BC的指向BA方向的向量bcPerp.
把AO投影到acPerp上, 如果投影为负, 那么原点不在单纯形内. 此时抛弃距原点最远的点B, 用点A和点C当作新的点A‘和点B‘, 重复以上过程.
把OB投影到bcPerp上, 如上判断原点是在BC内侧还是外侧. 如果是在BC外, 则抛弃离原点最远的A, 用B和C作为新的点A和B, 重复以上过程.
如果两个投影都为非负, 那么原点在单纯形ABC内, 判断两个图形重叠.
proc isIntersect*(s1, s2: Sprite2D): bool =
var
dir = Vector2D(x: 1, y: 0)
simplexA, simplexB, simplexC: Vector2D
simplexA = getSupportPoint(s1, s2, dir)
if simplexA * dir < 0: return false
dir = simplexA.negate()
simplexB = getSupportPoint(s1, s2, dir)
if simplexB * dir < 0: return false
let
ao = simplexA.negate()
ab = simplexB - simplexA
dir = tripleProduct(ab, ao, ab)
while true:
simplexC = getSupportPoint(s1, s2, dir)
if simplexC * dir < 0:
return false
let
ba = simplexA - simplexB
ac = simplexC - simplexA
bc = simplexC - simplexB
acPerp = tripleProduct(ac, ba.negate(), ac)
bcPerp = tripleProduct(bc, ba, bc)
if acPerp * simplexA > 0:
simplexB = simplexC
dir = acPerp.negate()
elif bcPerp * simplexB > 0:
simplexA = simplexC
dir = bcPerp.negate()
else: return true
上面的tripleProduct是连续两次叉乘, A×B×A会得到一个垂直于A的指向B方向的向量.
proc tripleProduct*(v1, v2, v3: Vector2D): Vector2D =
result.x = -(v1.x * v2.y - v1.y * v2.x) * v3.y
result.y = (v1.x * v2.y - v1.y * v2.x) * v3.x
GJK(Gilbert–Johnson–Keerthi) 判断任意凸图形是否重叠
原文:http://www.cnblogs.com/pngx/p/4395992.html