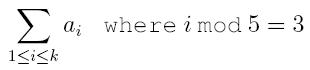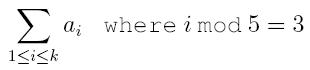http://acm.hdu.edu.cn/showproblem.php?pid=4288
Problem Description
In mathematics and computer science, an algorithm describes a set of procedures or instructions that define a procedure. The term has become increasing popular since the advent of cheap and reliable computers. Many companies now employ a single coder to write
an algorithm that will replace many other employees. An added benefit to the employer is that the coder will also become redundant once their work is done.
1
You are now the signle coder, and have been assigned a new task writing code, since your boss would like to replace many other employees (and you when you become redundant once your task is complete).
Your code should be able to complete a task to replace these employees who do nothing all day but eating: make the digest sum.
By saying “digest sum” we study some properties of data. For the sake of simplicity, our data is a set of integers. Your code should give response to following operations:
1. add x – add the element x to the set;
2. del x – remove the element x from the set;
3. sum – find the digest sum of the set. The digest sum should be understood by
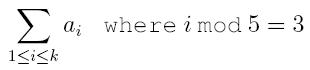
where the set S is written as {a
1, a
2, ... , a
k} satisfying a
1 < a
2 < a
3 < ... < a
k
Can you complete this task (and be then fired)?
------------------------------------------------------------------------------
1 See http://uncyclopedia.wikia.com/wiki/Algorithm
Input
There’re several test cases.
In each test case, the first line contains one integer N ( 1 <= N <= 105 ), the number of operations to process.
Then following is n lines, each one containing one of three operations: “add x” or “del x” or “sum”.
You may assume that 1 <= x <= 109.
Please see the sample for detailed format.
For any “add x” it is guaranteed that x is not currently in the set just before this operation.
For any “del x” it is guaranteed that x must currently be in the set just before this operation.
Please process until EOF (End Of File).
Output
For each operation “sum” please print one line containing exactly one integer denoting the digest sum of the current set. Print 0 if the set is empty.
Sample Input
9
add 1
add 2
add 3
add 4
add 5
sum
add 6
del 3
sum
6
add 1
add 3
add 5
add 7
add 9
sum
Sample Output
3
4
5
Hint
C++ maybe run faster than G++ in this problem.
/**
hdu4288 离线线段树
题目大意:对一个起初为空的数组进行三种操作:add x:插入x:del x:删除x:sum :查询在当前数列中下标对5取模为3的数的总和。
解题思路:暴力会超时。可以利用线段树来做,由于线段树不支持点的删除和增加,普通的在线线段树无法满足题目要求。我们可以把所有的在输入中增加过的点全部存上,
然后去重,组成一个序列,对于其中的元素如果当前线段树中有,那么就标记为1,否则为0,维护线段树中标记的个数cnt,以及对5取模的五种情况的值。
遇到添加、删除操作的时候,只要把那个节点的值改变,然后将它对下标的影响处理好就可以。
那么如何处理这些操作对下标的影响呢?
现在我们考虑一个父区间,假设它的左右子区间已经更新完毕。
显然,左区间中下标%5的情况与父区间中%5的情况完全相同;
可是,右区间中却不一定相同,因为右区间中的下标是以 mid 当作 1 开始的。
那么,只要我们知道左区间中有效元素的个数 cnt,我们就能知道右区间中的下标 i 在父区间中对应的下标为 i+cnt。
所以,虽然我们最终要的只是总区间中下标%5 = 3的和。但是在更新时我们需要知道右区间%5的所有情况。
于是我们要在线段树的每个节点开一个 sum[5] 和一个 cnt,分别记录这个节点中下标%5的5种情况的和与有效元素的个数。
而查询时,直接访问总区间的 sum[3] 即可。
*/
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;
typedef long long LL;
const int maxn=500000+10;
int n,len,flag;
char str[maxn][10];
int num[maxn],s[maxn];
struct node
{
int l,r,cnt;
LL sum[5];
}tree[maxn*4];
void init(int l,int r,int i)
{
tree[i].l=l;
tree[i].r=r;
tree[i].cnt=0;
memset(tree[i].sum,0,sizeof(tree[i].sum));
if(l!=r)
{
int mid=(l+r)>>1;
init(l,mid,i<<1);
init(mid+1,r,2*i+1);
}
}
void add(int x)
{
for(int i=0;i<5;i++)
{
int j=(i+tree[x<<1].cnt)%5;
tree[x].sum[j]=tree[x<<1].sum[j]+tree[x<<1|1].sum[i];
}
}
void insert(int i,int pos,int m)
{
flag?tree[i].cnt++:tree[i].cnt--;
if(tree[i].l==tree[i].r)
{
tree[i].sum[1]=flag*m;
return;
}
int mid=(tree[i].l+tree[i].r)>>1;
if(pos<=mid)
insert(i<<1,pos,m);
else
insert(i<<1|1,pos,m);
add(i);
}
int main()
{
while(~scanf("%d",&n))
{
len=0;
for(int i=0;i<n;i++)
{
scanf("%s",str[i]);
if(str[i][0]!='s')
{
scanf("%d",&num[i]);
s[len++]=num[i];
}
}
sort(s,s+len);
len=unique(s,s+len)-s;
if(len==0)
{
memset(tree[1].sum,0,sizeof(tree[1].sum));
}
else
{
init(1,len,1);
}
for(int i=0;i<n;i++)
{
if(str[i][0]=='a')
{
flag=1;
int pos=lower_bound(s,s+len,num[i])-s+1;
insert(1,pos,num[i]);
}
else if(str[i][0]=='d')
{
flag=0;
int pos=lower_bound(s,s+len,num[i])-s+1;
insert(1,pos,num[i]);
}
else
{
/*for(int j=0;j<5;j++)
printf("%I64d ",tree[1].sum[j]);
printf("\n");*/
printf("%I64d\n",tree[1].sum[3]);
}
}
}
return 0;
}
/**
18
add 1
add 2
add 3
add 4
add 5
sum
add 6
add 7
add 8
add 9
add 10
add 11
add 12
del 3
add 13
add 14
del 9
sum
answer:14
*/
Problem Description
In mathematics and computer science, an algorithm describes a set of procedures or instructions that define a procedure. The term has become increasing popular since the advent of cheap and reliable computers. Many companies now employ a single coder to write
an algorithm that will replace many other employees. An added benefit to the employer is that the coder will also become redundant once their work is done.
1
You are now the signle coder, and have been assigned a new task writing code, since your boss would like to replace many other employees (and you when you become redundant once your task is complete).
Your code should be able to complete a task to replace these employees who do nothing all day but eating: make the digest sum.
By saying “digest sum” we study some properties of data. For the sake of simplicity, our data is a set of integers. Your code should give response to following operations:
1. add x – add the element x to the set;
2. del x – remove the element x from the set;
3. sum – find the digest sum of the set. The digest sum should be understood by
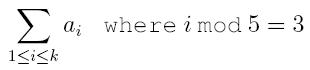
where the set S is written as {a
1, a
2, ... , a
k} satisfying a
1 < a
2 < a
3 < ... < a
k
Can you complete this task (and be then fired)?
------------------------------------------------------------------------------
1 See http://uncyclopedia.wikia.com/wiki/Algorithm
Input
There’re several test cases.
In each test case, the first line contains one integer N ( 1 <= N <= 105 ), the number of operations to process.
Then following is n lines, each one containing one of three operations: “add x” or “del x” or “sum”.
You may assume that 1 <= x <= 109.
Please see the sample for detailed format.
For any “add x” it is guaranteed that x is not currently in the set just before this operation.
For any “del x” it is guaranteed that x must currently be in the set just before this operation.
Please process until EOF (End Of File).
Output
For each operation “sum” please print one line containing exactly one integer denoting the digest sum of the current set. Print 0 if the set is empty.
Sample Input
9
add 1
add 2
add 3
add 4
add 5
sum
add 6
del 3
sum
6
add 1
add 3
add 5
add 7
add 9
sum
Sample Output
3
4
5
Hint
C++ maybe run faster than G++ in this problem.
hdu4288 离线处理线段树
原文:http://blog.csdn.net/lvshubao1314/article/details/44906367