这篇也是之前写在知乎上的一个答案,不过后来发现答非所问,无所谓,在这重新总结一下。线性时不变系统和信号响应是信号与系统理论中两个非常基本的观点,从线性代数的角度理解起来非常清晰。首先,来看线性代数中的一个非常基本的概念:
线性映射(Linear Map)
设想有个向量v,通过某种映射可以从v得到w,记为w=T\left( v \right)
1)
T\left( u+v \right)=T\left( u \right)+T\left( v
\right)
2) aT\left( v \right)=T\left( av
\right)
那么就称T是一个线性映射。其实说通俗了就是简单的加法而已。从信号与系统的观点看来,如果我们把输入信号和输出信号分别和v和w对应起来的话,似乎就是个简单的线性映射系统啊。当然实际上没有这么简单,还多了那么一点东西,所以在信号与系统里,叫做:
线性时不变(Linear Time-Invariant, LTI)系统
什么叫时不变呢?以冲击函数为例子说明一下,假设在t=0的位置上有个单位冲击,在某个LTI
system中,造成的响应是在t=1到t=2区间上的某种曲线。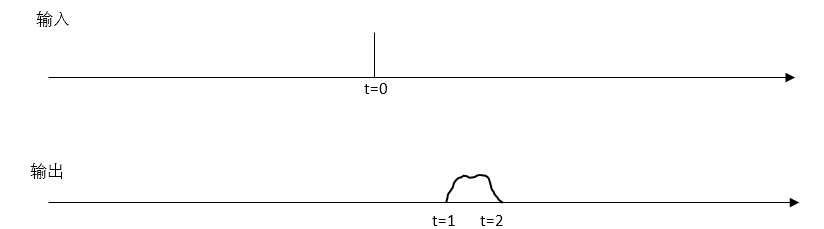
时不变的意思就是如果把这个t=0上的单位冲击移动到任意时间点,比如t0去,那么响应的曲线也会响应地移动到t=t0+1到t=t0+2的位置上去。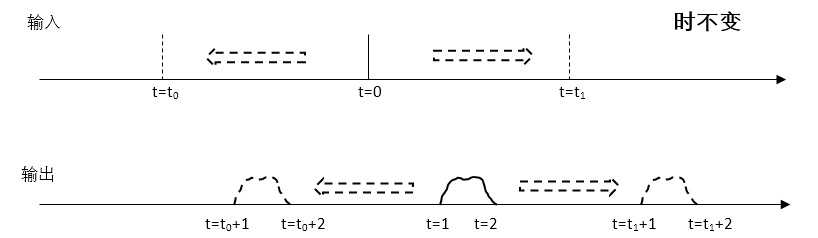
结合之前线性系统的定义,整个系统是线性的,所以是线性+时不变。简单来说就是输入信号怎么个叠加法,输出信号就怎么叠加。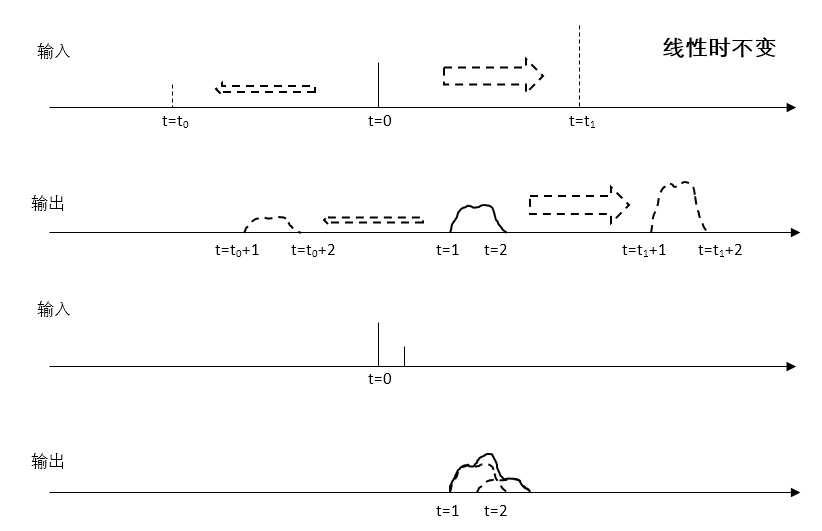
其实从线性代数角度也可以理解线性时不变系统,本质还是线性映射。比如考虑对如下对一个向量的变换:
\left( \begin{matrix} 0 \\
0 \\ x \\ 0 \\
\end{matrix} \right)=\left( \begin{matrix} 0 & 0 & 0 &
0 \\ 1 & 0 & 0 & 0 \\ 0 &
1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\
\end{matrix} \right)\left( \begin{matrix} 0 \\
x \\ 0 \\ 0 \\ \end{matrix}
\right)
信号响应
了解了线性时不变系统,由卷积求信号的响应的方法就可以看成是一个线性系统中的叠加,说白了就是简简单单的加法而已:已知冲激信号在输出中的响应的情况下,给定一个输入信号,只要把输入信号看成一个个时间点上的冲激信号的叠加,直接在输出的t时间点上把这所有冲激信号的响应简单加起来,就可以了。图形化的例子就是上面讲线性时不变部分里的最后一个示意图。
写出来的话就是:
\cdots +f\left( n-1 \right)h\left( t-\left( n-1 \right)
\right)+f\left( n \right)h\left( t-n \right)+f\left( n+1 \right)h\left( t-\left(
n+1 \right) \right)+\cdots =\sum\limits_{\tau }{f\left( \tau
\right)}h\left( t-\tau \right)=f*h\left( t \right)
从线性代数的角度理解线性时不变系统和信号响应,布布扣,bubuko.com
原文:http://www.cnblogs.com/frombeijingwithlove/p/3594272.html