1 #include<iostream> 2 #include<cstdio> 3 #include<ctime> 4 using namespace std; 5 #define M 4 6 #define N 4 7 #include <memory.h> 8 9 int maxSubArray(int *arr, int len) //最大子序列和 10 { 11 int i, sum = arr[0], b = 0; 12 for (i = 0; i<len; ++i) 13 { 14 if (b>0) 15 b += arr[i]; 16 else 17 b = arr[i]; 18 if (b>sum) 19 sum = b; 20 } 21 return sum; 22 } 23 int maxSubMatrix(int n, int m, int array[M][N]) 24 { 25 int i, j, h, max, sum = -100000; 26 int b[100]; 27 for (i = 0; i<n; i++) 28 { 29 memset(b, 0, sizeof(b)); //初始化b[] 30 for (j = i; j<n; j++) //把第i行到第j行相加,对每一次相加求出最大值 31 { 32 for (h = 0; h<m; h++) 33 { 34 b[h] += array[j][h]; //二维数组压缩成一维数组,然后求最大子序列和 35 } 36 max = maxSubArray(b, h); 37 38 if (max>sum) 39 sum = max; 40 } 41 } 42 return sum; 43 } 44 int main() 45 { 46 int arr[M][N]; 47 cout << "随机二维数组为:" << endl; 48 srand(time(0)); 49 for (int i = 0; i < M; i++) 50 { 51 for (int j = 0; j < N; j++) 52 { 53 arr[i][j] = rand() % 50-25; 54 cout << arr[i][j] << " "; 55 } 56 cout << endl; 57 } 58 cout << maxSubMatrix(M, N, arr) << endl; 59 return 0; 60 }
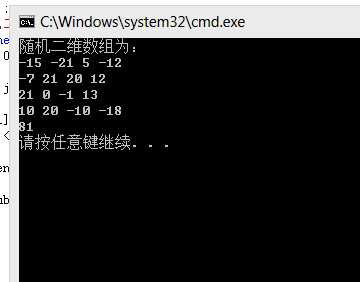
因为原代码是引用Txt文件中的数组,为产生随机数做出改动,在引用参数时出现int类型的实参与int 类型的形参不兼容的错误,通过网上查找资料改正。
总结:通过看网络上前辈们的代码,将他们代码的思路和自己的思路进行比较,找出自己的不足,并通过实际敲代码来体会这种差别,受益良多。
原文:http://www.cnblogs.com/SanShaoS/p/4412525.html