骨牌,一种古老的玩具。今天我们要研究的是骨牌的覆盖问题:
我们有一个2xN的长条形棋盘,然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘,一共有多少种不同的覆盖方法呢?
举个例子,对于长度为1到3的棋盘,我们有下面几种覆盖方式:
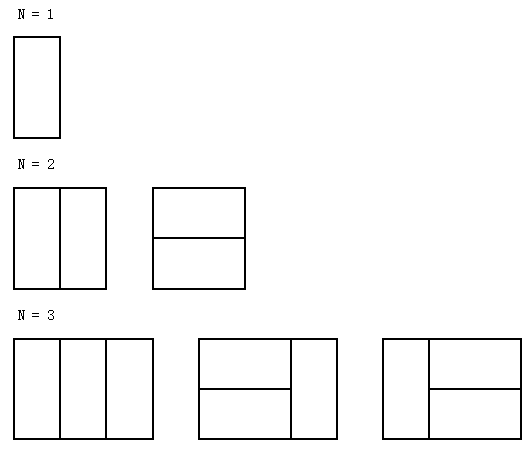
第1行:1个整数N。表示棋盘长度。1≤N≤100,000,000
第1行:1个整数,表示覆盖方案数 MOD 19999997
62247088
17748018
代码:
1 /*快速矩阵*/ 2 #include<iostream> 3 #define _int long long 4 const _int mod = 19999997; 5 using namespace std; 6 7 struct GMagin { 8 9 long long Margin [2][2]; 10 11 }Gbase,Gbasa; 12 13 /* 14 |f(n) | = |f(n-1)| * |1,1| 15 |f(n-1)| |f(n-2)| |1,0| 16 */ 17 18 void init(GMagin &Gbase ,int a=1,int b=1,int c=1,int d=0) { 19 20 Gbase.Margin[0][0] = a; 21 Gbase.Margin[0][1] = b; 22 Gbase.Margin[1][0] = c; 23 Gbase.Margin[1][1] = d; 24 } 25 26 /*快速矩阵算法*/ 27 void Marginal(GMagin & a , GMagin &b ) { 28 GMagin res; 29 init(res,0,0,0,0); 30 for (int i = 0; i < 2; i++) { 31 for (int j = 0; j < 2; j++) { 32 for (int k = 0; k < 2; k++) 33 res.Margin[i][j] = (res.Margin[i][j]+a.Margin[i][k] * b.Margin[k][j])%mod; 34 } 35 } 36 init(a ,res.Margin[0][0], res.Margin[0][1], res.Margin[1][0], res.Margin[1][1]); 37 } 38 void matpow(int n) { 39 40 while (n > 0) { 41 if (n & 1) Marginal(Gbase,Gbasa); 42 n>>=1L; 43 if (n == 0) break; 44 Marginal(Gbasa, Gbasa); 45 } 46 } 47 48 int main(int argc ,char * argv []) { 49 50 int n; 51 while (cin>>n) { 52 init(Gbase); 53 init(Gbasa); 54 int res; 55 if (n > 2) { 56 matpow(n - 2); 57 res = (Gbase.Margin[0][0] + Gbase.Margin[0][1]) % mod; 58 } 59 else { 60 61 if (n == 0 || n == 1)res = 1; 62 else if (n == 2) res = 2; 63 } 64 cout << res << endl; 65 } 66 return 0; 67 }
原文:http://www.cnblogs.com/gongxijun/p/4418625.html