今天刚掌握Kruskal算法,写下随笔。
对于稀疏图来说,用Kruskal写最小生成树效率更好,加上并查集,可对其进行优化。
Kruskal算法的步骤:
1.对所有边进行从小到大的排序。
2.每次选一条边(最小的边),如果如果形成环,就不加入(u,v)中,否则加入。那么加入的(u,v)一定是最佳的。
并查集:
我们可以把每个连通分量看成一个集合,该集合包含了连通分量的所有点。而具体的连通方式无关紧要,好比集合中的元素没有先后顺序之分,只有“属于”与“不属于”的区别。图的所有连通分量可以用若干个不相交集合来表示。
而并查集的精妙之处在于用数来表示集合。如果把x的父结点保存在p[x]中(如果没有父亲,p[x]=x),则不难写出结点x所在树的递归程序:
find(int x) {return p[x]==x?x:p[x]=find(p[x]);}
意思是,如果p[x]=x,说明x本身就是树根,因此返回x;否则返回x的父亲p[x]所在树的根结点。
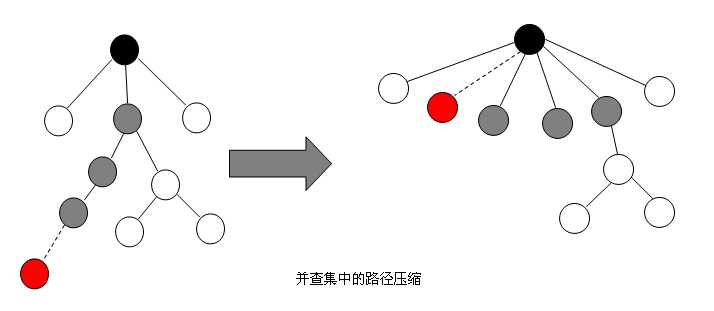
既然每棵树表示的只是一个集合,因此树的形态是无关紧要的,并不需要在“查找”操作之后保持树的形态不变,只要顺便把遍历过的结点都改成树根的儿子,下次查找就会快很多了。如下图所示:

1 //hdu_1863 2 #include <stdio.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #define N 150 6 using namespace std; 7 int m,n,u[N],v[N],w[N],p[N],r[N]; 8 int cmp(const int i,const int j) {return w[i]<w[j];} 9 int find(int x) {return p[x]==x?x:p[x]=find(p[x]);} 10 int kruskal() 11 { 12 int cou=0,x,y,i,ans=0; 13 for(i=0;i<n;i++) p[i]=i; 14 for(i=0;i<m;i++) r[i]=i; 15 sort(r,r+m,cmp); 16 for(i=0;i<m;i++) 17 { 18 int e=r[i];x=find(u[e]);y=find(v[e]); 19 if(x!=y) {ans += w[e];p[x]=y;cou++;} 20 } 21 if(cou<n-1) ans=0; 22 return ans; 23 } 24 25 int main() 26 { 27 int i,ans; 28 while(scanf("%d%d",&m,&n)!=EOF&&m) 29 { 30 for(i=0;i<m;i++) 31 { 32 scanf("%d%d%d",&u[i],&v[i],&w[i]); 33 } 34 ans=kruskal(); 35 if(ans) printf("%d\n",ans); 36 else printf("?\n",ans); 37 } 38 return 0; 39 }
我的hdu1863代码:
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1863
1 #include <cstdio> 2 #include <iostream> 3 #include <cstring> 4 //#include <algotithm> 5 #include <stdlib.h> 6 using namespace std; 7 typedef struct IN 8 { 9 int a; 10 int b; 11 int c; 12 }IN; 13 IN s[5000]; 14 int N,M; 15 int pre[110]; 16 int cmp(const void *a,const void *b) 17 { 18 return (*(IN *)a).c - (*(IN *)b).c; 19 } 20 int find(int x) 21 { 22 int i,r,t; 23 r=x; 24 while(r!=pre[r]) 25 r=pre[r]; 26 while(x!=r) 27 { 28 i=pre[x]; 29 pre[x]=r; 30 x=i; 31 } 32 return r; 33 } 34 int kruskal() 35 { 36 int i,j,pa,pb,num=0,sum=0; 37 for(i=0;i<=M;i++) 38 pre[i]=i; 39 for(i=0;i<N;i++) 40 { 41 pa=find(s[i].a); 42 pb=find(s[i].b); 43 if(pa!=pb) 44 { 45 pre[pa]=pb; 46 sum+=s[i].c; 47 num++; 48 } 49 } 50 if(num==M-1) 51 return sum; 52 else 53 return 0; 54 } 55 int main() 56 { 57 while(scanf("%d %d",&N,&M),N) 58 { 59 int i,j,t; 60 memset(s,0,sizeof(s)); 61 for(i=0;i<N;i++) 62 scanf("%d %d %d",&s[i].a,&s[i].b,&s[i].c); 63 qsort(s,N,sizeof(s[0]),cmp); 64 //for(i=0;i<N;i++) 65 //printf("%d\n",s[i].c); 66 t=kruskal(); 67 if(t) 68 printf("%d\n",t); 69 else 70 printf("?\n"); 71 } 72 return 0; 73 }
原文:http://www.cnblogs.com/xl1027515989/p/3597091.html