直接说几个比较明显的规律吧。
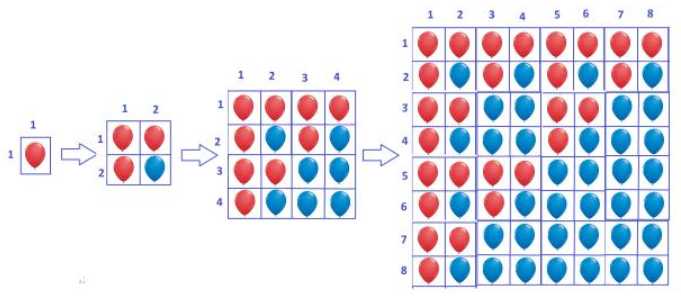
k个小时以后,红气球的个数为3k。
单独观察一行:
令f(r, k)为k个小时后第r行红气球的个数。
令g(r, k)为k个小时后前r行红气球的个数。
因此f和g都可以用递归求解。

1 #include <cstdio> 2 typedef long long LL; 3 4 LL f(LL r, LL k) 5 { 6 if(k == 0) return 1LL; 7 if(r & 1LL) return f((r+1)/2 ,k-1) * 2; 8 else return f(r/2, k-1); 9 } 10 11 LL g(LL r, LL k) 12 { 13 if(r == 0) return 0; 14 if(k == 0) return 1LL; 15 LL ans = g(r/2, k-1) * 3; 16 if(r & 1) ans += f(r, k); 17 return ans; 18 } 19 20 int main() 21 { 22 int T; scanf("%d", &T); 23 for(int kase = 1; kase <= T; kase++) 24 { 25 LL k, a, b; 26 scanf("%lld%lld%lld", &k, &a, &b); 27 printf("Case %d: %lld\n", kase, g(b, k) - g(a-1, k)); 28 } 29 30 return 0; 31 }
UVa 12627 (递归 计数 找规律) Erratic Expansion
原文:http://www.cnblogs.com/AOQNRMGYXLMV/p/4421988.html