如何用C语言画一个圣诞树？

时间：2015-04-19 14:36:14 阅读：319 评论：0 收藏：0 [点我收藏+]

我使用了左右镜像的Sierpinski triangle，每层减去上方一小块，再用符号点缀。可生成不同层数的「圣诞树」，如下图是5层的结果。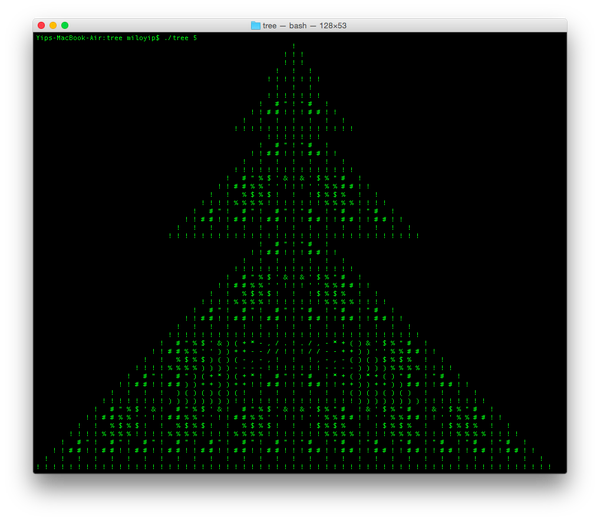

#include <stdio.h>
#include <stdlib.h>

int main(int argc, char* argv[]) {
    int n = argc > 1 ? atoi(argv[1]) : 4;
    for (int j = 1; j <= n; j++) {
        int s = 1 << j, k = (1 << n) - s, x;
        for (int y = s - j; y >= 0; y--, putchar(‘\n‘)) {
            for (x = 0; x < y + k; x++) printf("  ");
            for (x = 0; x + y < s; x++) printf("%c ", ‘!‘ ^ y & x);
            for (x = 1; x + y < s; x++) printf("%c ", ‘!‘ ^ y & (s - y - x - 1));
        }
    }
}

基本代码来自Sierpinski triangle的实现，字符的想法来自于code golf - Draw A Sierpinski Triangle。
--
更新1: 上面的是我尝试尽量用最少代码来画一个抽象一点的圣诞树，因此树干都没有。然后，我尝试用更真实一点的风格。因为树是一个比较自相似的形状，这次使用递归方式描述树干和分支。

n = 0的时候，就是只画一主树干，树干越高就越幼：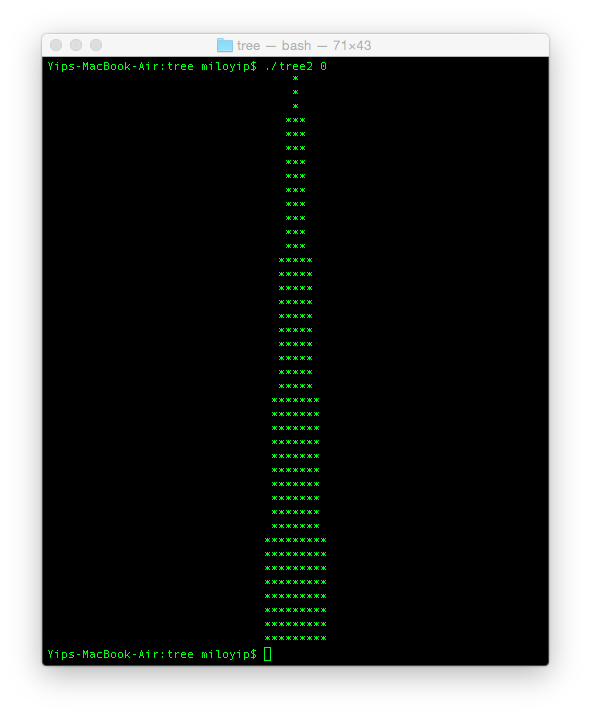

n = 1的时候，利用递归画向两面分支，旋转，越高的部分缩得越小。

n = 2 的时候，继续分支出更细的树支。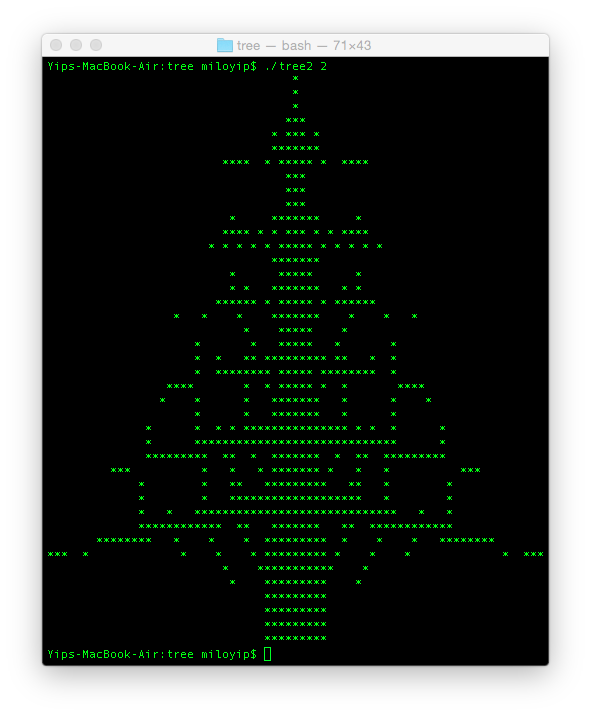

n = 3就差不多够细节了。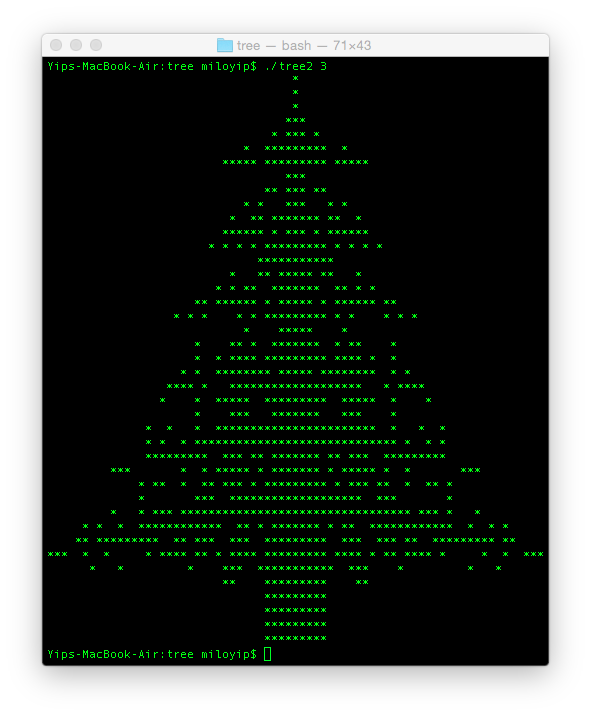

代码长一点，为了容易理解我不「压缩」它了。

#include <math.h>
#include <stdio.h>
#include <stdlib.h>

#define PI 3.14159265359

float sx, sy;

float sdCircle(float px, float py, float r) {
    float dx = px - sx, dy = py - sy;
    return sqrtf(dx * dx + dy * dy) - r;
}

float opUnion(float d1, float d2) {
    return d1 < d2 ? d1 : d2;
}

#define T px + scale * r * cosf(theta), py + scale * r * sin(theta)

float f(float px, float py, float theta, float scale, int n) {
    float d = 0.0f;
    for (float r = 0.0f; r < 0.8f; r += 0.02f)
        d = opUnion(d, sdCircle(T, 0.05f * scale * (0.95f - r)));

    if (n > 0)
        for (int t = -1; t <= 1; t += 2) {
            float tt = theta + t * 1.8f;
            float ss = scale * 0.9f;
            for (float r = 0.2f; r < 0.8f; r += 0.1f) {
                d = opUnion(d, f(T, tt, ss * 0.5f, n - 1));
                ss *= 0.8f;
            }
        }

    return d;
}

int main(int argc, char* argv[]) {
    int n = argc > 1 ? atoi(argv[1]) : 3;
    for (sy = 0.8f; sy > 0.0f; sy -= 0.02f, putchar(‘\n‘))
        for (sx = -0.35f; sx < 0.35f; sx += 0.01f)
            putchar(f(0, 0, PI * 0.5f, 1.0f, n) < 0 ? ‘*‘ : ‘ ‘);
}

这段代码实际上是用了圆形的距离场来建模，并且没有优化。

这是一棵「婐树」，未能称得上是「圣诞树」。

--
更新2: 简单地加入装饰及丝带，在命令行可以选择放大倍率，下图是两倍大的。

// f() 及之前的部分沿上

int ribbon() {
    float x = (fmodf(sy, 0.1f) / 0.1f - 0.5f) * 0.5f;
    return sx >= x - 0.05f && sx <= x + 0.05f;
}

int main(int argc, char* argv[]) {
    int n = argc > 1 ? atoi(argv[1]) : 3;
    float zoom = argc > 2 ? atof(argv[2]) : 1.0f;
    for (sy = 0.8f; sy > 0.0f; sy -= 0.02f / zoom, putchar(‘\n‘))
        for (sx = -0.35f; sx < 0.35f; sx += 0.01f / zoom) {
            if (f(0, 0, PI * 0.5f, 1.0f, n) < 0.0f) {
                if (sy < 0.1f)
                    putchar(‘.‘);
                else {
                    if (ribbon())
                        putchar(‘=‘);
                    else
                        putchar("............................#j&o"[rand() % 32]);
                }
            }
            else
                putchar(‘ ‘);
        }
}

2D的我想已差不多了。接下来看看有没有空尝试3D的。

--
更新3：终于要3D了。之前每个节点是往左和右分支，在三维中我们可以更自由一点，我尝试在每个节点申出6个分支。最后用了简单的Lambertian着色（即max(dot(N, L), 0）。

n = 1 的时候比较容易看出立体的着色：

可是n=3的时候已乱得难以辨认：

估计是因为aliasing而做成的。由于光照已经使用了finite difference来计算法线，性能已经很差，我就不再尝试做Supersampling去解决aliasing的问题了。另外也许Ambient occlusion对这问题也有帮助，不过需要更多的采样。

因为需要三维旋转，不能像二维简单使用一个角度来代表旋转，所以这段代码加入了不少矩阵运算。当然用四元数也是可以的。

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define PI 3.14159265359f

float sx, sy;

typedef float Mat[4][4];
typedef float Vec[4];

void scale(Mat* m, float s) {
    Mat temp = { {s,0,0,0}, {0,s,0,0 }, { 0,0,s,0 }, { 0,0,0,1 } };
    memcpy(m, &temp, sizeof(Mat));
}

void rotateY(Mat* m, float t) {
    float c = cosf(t), s = sinf(t);
    Mat temp = { {c,0,s,0}, {0,1,0,0}, {-s,0,c,0}, {0,0,0,1} };
    memcpy(m, &temp, sizeof(Mat));
}

void rotateZ(Mat* m, float t) {
    float c = cosf(t), s = sinf(t);
    Mat temp = { {c,-s,0,0}, {s,c,0,0}, {0,0,1,0}, {0,0,0,1} };
    memcpy(m, &temp, sizeof(Mat));
}

void translate(Mat* m, float x, float y, float z) {
    Mat temp = { {1,0,0,x}, {0,1,0,y}, {0,0,1,z}, {0,0,0,1} };
    memcpy(m, &temp, sizeof(Mat));
}

void mul(Mat* m, Mat a, Mat b) {
    Mat temp;
    for (int j = 0; j < 4; j++)
        for (int i = 0; i < 4; i++) {
            temp[j][i] = 0.0f;
            for (int k = 0; k < 4; k++)
                temp[j][i] += a[j][k] * b[k][i];
        }
    memcpy(m, &temp, sizeof(Mat));    
}

void transformPosition(Vec* r, Mat m, Vec v) {
    Vec temp = { 0, 0, 0, 0 };
    for (int j = 0; j < 4; j++)
        for (int i = 0; i < 4; i++)
            temp[j] += m[j][i] * v[i];
    memcpy(r, &temp, sizeof(Vec));    
}

float transformLength(Mat m, float r) {
    return sqrtf(m[0][0] * m[0][0] + m[0][1] * m[0][1] + m[0][2] * m[0][2]) * r;
}

float sphere(Vec c, float r) {
    float dx = c[0] - sx, dy = c[1] - sy;
    float a = dx * dx + dy * dy;
    return a < r * r ? sqrtf(r * r - a) + c[2] : -1.0f;
}

float opUnion(float z1, float z2) {
    return z1 > z2 ? z1 : z2;
}

float f(Mat m, int n) {
    float z = -1.0f;
    for (float r = 0.0f; r < 0.8f; r += 0.02f) {
        Vec v = { 0.0f, r, 0.0f, 1.0f };
        transformPosition(&v, m, v);
        z = opUnion(z, sphere(v, transformLength(m, 0.05f * (0.95f - r))));
    }

    if (n > 0) {
        Mat ry, rz, s, t, m2, m3;
        rotateZ(&rz, 1.8f);

        for (int p = 0; p < 6; p++) {
            rotateY(&ry, p * (2 * PI / 6));
            mul(&m2, ry, rz);
            float ss = 0.45f;
            for (float r = 0.2f; r < 0.8f; r += 0.1f) {
                scale(&s, ss);
                translate(&t, 0.0f, r, 0.0f);
                mul(&m3, s, m2);
                mul(&m3, t, m3);
                mul(&m3, m, m3);
                z = opUnion(z, f(m3, n - 1));
                ss *= 0.8f;
            }
        }
    }

    return z;
}

float f0(float x, float y, int n) {
    sx = x;
    sy = y;
    Mat m;
    scale(&m, 1.0f);
    return f(m, n);
}

int main(int argc, char* argv[]) {
    int n = argc > 1 ? atoi(argv[1]) : 3;
    float zoom = argc > 2 ? atof(argv[2]) : 1.0f;
    for (float y = 0.8f; y > -0.0f; y -= 0.02f / zoom, putchar(‘\n‘))
        for (float x = -0.35f; x < 0.35f; x += 0.01f / zoom) {
            float z = f0(x, y, n);
            if (z > -1.0f) {
                float nz = 0.001f;
                float nx = f0(x + nz, y, n) - z;
                float ny = f0(x, y + nz, n) - z;
                float nd = sqrtf(nx * nx + ny * ny + nz * nz);
                float d = (nx - ny + nz) / sqrtf(3) / nd;
                d = d > 0.0f ? d : 0.0f;
                // d = d < 1.0f ? d : 1.0f;
                putchar(".-:=+*#%@@"[(int)(d * 9.0f)]);
            }
            else
                putchar(‘ ‘);
        }
}

--
更新4：发现之前的TransformLength()写错了，上面已更正。另外，考虑提升性能时，一般是需要一些空间剖分的方式去加速检查，但这里刚好是一个树状的场景结构，可以简单使用Bounding volume hierarchy，我使用了球体作为包围体积。只需加几句代码，便可以大大缩减运行时间。

另外，考虑到太小的叶片是很难采样得到好看的结果，我尝试以一个较大的球体去表现叶片（就如素描时考虑更整体的光暗而不是每片叶片的光暗），我觉得结果有进步。

float f(Mat m, int n) {
    // Culling
    {
        Vec v = { 0.0f, 0.5f, 0.0f, 1.0f };
        transformPosition(&v, m, v);        
        if (sphere(v, transformLength(m, 0.55f)) == -1.0f)
            return -1.0f;
    }

    float z = -1.0f;

    if (n == 0) { // Leaf
        Vec v = { 0.0f, 0.5f, 0.0f, 1.0f };
        transformPosition(&v, m, v);        
        z = sphere(v, transformLength(m, 0.3f));
    }  
    else { // Branch
        for (float r = 0.0f; r < 0.8f; r += 0.02f) {
            Vec v = { 0.0f, r, 0.0f, 1.0f };
            transformPosition(&v, m, v);
            z = opUnion(z, sphere(v, transformLength(m, 0.05f * (0.95f - r))));
        }
    }

    // ...
}

其实我在回答这问题的时候，并没有计划，只是一步一步地尝试。现在我觉得用这规模的代码大概不能再怎么进展了。不过今天看到大堂里的圣诞树，觉得那些装饰物还挻有趣的，有时候除了画整体，也可以画局部，看看是否能再更新。