一 题目:一个首尾相接的二维数组,其中有有正数,有负数,求它的最大子矩阵。
二 设计思路:
这道题基本无难度,因为这道题可以参考以前做过的求解二维数组的子矩阵(不是首尾相接),所以可以简单划分为两部分。第一步先将它化为一维首尾相接的数组(环),然后再利用求解环中最大子数组的思想求解。具体将二维数组化为一维数组请参考(http://www.cnblogs.com/houtaoliang/p/4401630.html),在此只简单分析求解环的最大子数组。
求解环的最大子数组可分为两种情况。第一种:当数组下标没有越界,举例说明,如 -2 1 5 9 -6 4,最大子数组为1 5 9。这时可以利用动态规划的思想求解。假设最大子数组为a[i]--a[j-1],令sum=a[i]+..+a[j-1],若它为最大子数组则必有sun+a[j]>a[j]即sum>0,否则令a[j]赋值给sum。第二种情况是数组越界时,如 1 3 2 -9 -4 6
此时就相当于求解数组中的最小子数组(和求最大子数组原理一样),再用全部数组和减去这个最小子数组,就得到了最大子数组。
三 代码
#include<iostream> using namespace std; int MAX(int s[],int n) { int i,sum=0,max=s[0]; for(i=0;i<n;i++) { if(sum>0) { sum=sum+s[i]; } else { sum=s[i]; } if(sum>max) { max=sum; } } return max; } int MIN(int s[],int n) { int i,sum=0,min=s[0]; for(i=1;i<n;i++) { if(sum<0) { sum=sum+s[i]; } else { sum=s[i]; } if(sum<min) { min=sum; } } return min; } int SUM(int s[],int n) { int i,sum=0; for(i=0;i<n;i++) { sum=sum+s[i]; } return sum; } void main() { int m,n,i,j,a[100][100]; cout<<"请输入矩阵的大小(m*n):"; cin>>m>>n; cout<<"请输入矩阵:"<<endl; for(i=0;i<m;i++) { for(j=0;j<n;j++) { cin>>a[i][j]; } } int sum,max,s[100],k=0,min,p=a[0][0]; for(i=0;i<m;i++) { for(j=0;j<n;j++) { s[j]=0; } while(k+i<m) { for(j=0;j<n;j++) { s[j]=s[j]+a[k+i][j]; } sum=SUM(s,n); min=MIN(s,n); max=MAX(s,n); if(sum-min>max) { max=sum-min; } if(max>p) { p=max; } k++; } k=0; } cout<<"子矩阵最大值为"<<p<<endl; }
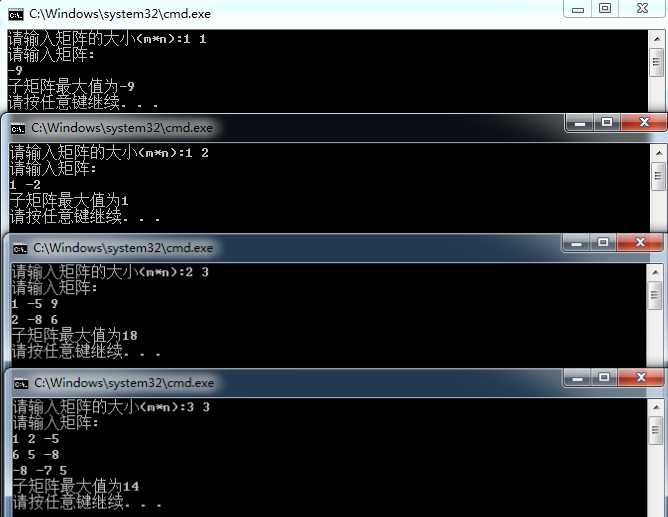
四 截图
原文:http://www.cnblogs.com/houtaoliang/p/4439345.html