一、题目和要求
二,思路
基本实现可以采用枚举法,即每到一个楼层,就要计算出所有人上下的情况,将所有人上下楼层数和相加然后求出其中最小值。但是,如果采用这种方式,代码时间复杂度较高,为O(n^2),于是我采用了上课老师讲述的方法。
具体设计思路:假设想去往第i-1层,第i层,第i+1层的学生人数分别为N2,N1,N3。设电梯停在第i层,则所有人的爬楼总和为Y=N2+N3;依次类推,若电梯停在第i-1层,爬楼总和为Y-N2+N1+N3;若电梯停在第i+1层,爬楼总和为Y-N3+N1+N2;
假设电梯停在第i层最好。
当Y>Y-N2+N1+N3,即N2-N1-N3<0,即N1+N3<N2,电梯停在第i-1层较好。
当Y>Y-N3+N1+N2,即N3-N2-N1>0,即N1+N2<N3,电梯停在第i+1层较好。
三,实现代码
#include <iostream.h>
#include<conio.h>
void dianti(int Arr[]);
int main()
{
int max = 18;//电梯的最高楼层为18层
int man[20];//电梯内最多能承载20人
int min,stop;//最小爬楼数,和电梯应停的楼层数
int N1,N2,N3;
int jixu;
min=0;
stop = 1; for(int i=0;i<20;i++)
{
man[i]=0;
}
dianti(man);
N1 = N3 = 0;
N2 = man[1];
for( i = 2; i <= max; i++)
{
N3 += man[i];
min=min+ man[i] * (i-1);
}
for( i=2;i<=max;i++)
{
if(N1 + N2 < N3)
{
stop = i;
min=min+(N1 + N2 - N3);
N1 += N2;
N2 = man[i];
N3 =N3- man[i];
}
else
{
break;
}
}
cout<<"电梯应停在第"<<stop<<"层"<<endl;
cout<<"所有人爬楼最小层数和为"<<min<<"层"<<endl;
cout<<"要继续测试吗?jixu(0,退出 1,继续)"<<endl; cin>>jixu; if(jixu==1) { cout<<endl; main(); } else { return 0;
} getch(); return 0;
} void dianti(int Arr[])
{
int n;
cout<<"请输入一层时电梯内人数:";
cin>>n;
int *a=new int[n];
cout<<"请输入每个人所按的楼梯层数:";
for(int i=0;i<n;i++)
{
cin>>a[i];
Arr[a[i]]=Arr[a[i]]+1;
} }
四,实验结果
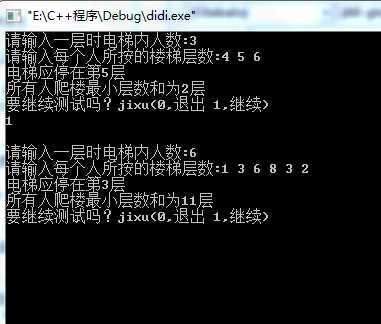
五,实验总结
这次实验开始时没有明确思路,但老师上课讲的思路听明白了,所以就按老师上课讲的思路进行编程。最终完成了本次实验。
原文:http://www.cnblogs.com/xiaojin123/p/4439586.html