Mean:
给你一个长度不超过1e6的数字串,求第k大的环状数字串的前面那个位置。
analyse:
好吧,我承认这是个水题,比赛的时候sb了,因为原来做过后缀自动机求解字符串的环状最小表示法,所以一直用后缀自动机的知识去套k小表示法,比赛的时候太固执了。
这题就是后缀数组的sa[]数组的运用,sa[i]=k表示的是字符串所有的后缀按字典序排序后,第i个后缀排在第k个。
那么我们只需将数字串复制一遍接在原串后面(环状),对s求一遍后缀数字得到sa数组,然后找到sa<=n的第k个sa,那么sa[i]-1就是答案。
为什么?看这张图:
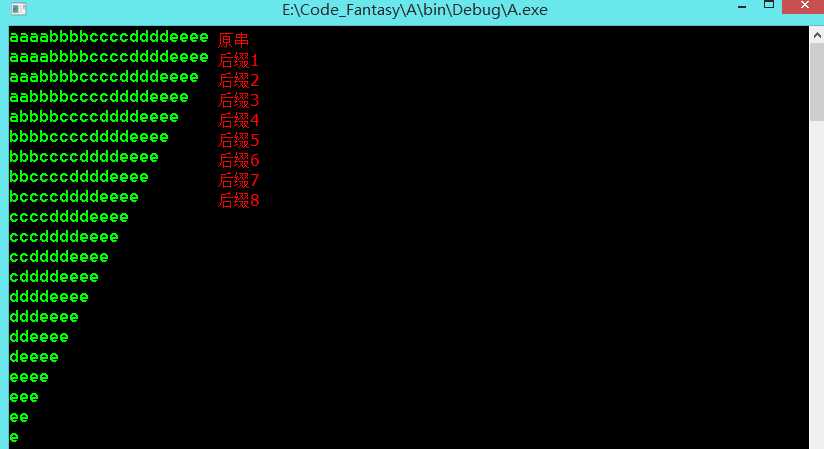
连接后的字符串我们可以得到2*n个字符串,但是我们只需关心前n个字符串就可,因为后面的n个字符串其实根本没作用,他们只相当于前n个字符串的前缀的重复出现而已。
所以我们只需要找到满足sa[i]<=n的第k个就行,sa[i]-1就是答案。
Time complexity: O(n)
Source code:

// Memory Time // 1347K 0MS // by : crazyacking // 2015-04-20-19.00 #include<map> #include<queue> #include<stack> #include<cmath> #include<cstdio> #include<vector> #include<string> #include<cstdlib> #include<cstring> #include<climits> #include<iostream> #include<algorithm> #define MAXN 1000010 #define LL long long using namespace std; const int maxn = 2002000; int Rank[maxn],wb[maxn],wv[maxn],wss[maxn]; bool cmp(int *r,int a,int b,int l) { return r[a]==r[b] && r[a+l]==r[b+l]; } void da(int *r,int *sa,int n,int m) { int i,j,p,*x=Rank,*y=wb,*t; for(i=0;i<m;i++) wss[i]=0; for(i=0;i<n;i++) wss[x[i]=r[i]]++; for(i=1;i<m;i++) wss[i]+=wss[i-1]; for(i=n-1;i>=0;i--) sa[--wss[x[i]]]=i; for(j=1,p=1;p<n;j*=2,m=p) { for(p=0,i=n-j;i<n;i++) y[p++]=i; for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j; for(i=0;i<n;i++) wv[i]=x[y[i]]; for(i=0;i<m;i++) wss[i]=0; for(i=0;i<n;i++) wss[wv[i]]++; for(i=1;i<m;i++) wss[i]+=wss[i-1]; for(i=n-1;i>=0;i--) sa[--wss[wv[i]]]=y[i]; for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++) x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++; } return; } char s[maxn]; int r[maxn],sa[maxn]; int main() { int n,k; while(~scanf("%d %d",&n,&k)) { getchar(); gets(s); int len = strlen(s),i; for(int i=len;i<len*2;++i) s[i]=s[i-len]; s[len*2]=‘\0‘; len=len*2; for(int i=0;i<len;++i) s[i]+=‘a‘-‘0‘; len++; for(i=0; i<len-1; i++) r[i] = s[i]-‘a‘+1; r[len-1] = 0; da(r,sa,len,30); int idx=0; for(int i=1;i<len;++i) { if(sa[i]+1<=n) { idx++; if(idx==k) printf("%d\n",sa[i]!=0?sa[i]:n); } } } return 0; }
后缀数组 --- WOj 1564 Problem 1564 - A - Circle
原文:http://www.cnblogs.com/crazyacking/p/4442386.html