文件下载http://files.cnblogs.com/files/tenlee/gw_netflow.pdf
给定一个有向图G=(V,E),把图中的边看作管道,每条边上有一个权值,表示该管道的流量上限。给定源点s和汇点t,现在假设在s处有一个水源,t处有一个蓄水池,
问从s到t的最大水流量是多少网络流图里,源点流出的量,等于汇点流入的量,除源汇外的任何点,其流入量之和等于流出两之和
解决最大流的Ford-Fulkerson算法
基本思路很简单,每次用dfs从源到汇找一条可行路径, 然后把这条路塞满。这条路径上容量最小的那条边的容量,就是这次dfs所找到的流量。然后对于路径上的每条边,其容量要减去刚才找到的流量。这样,每次dfs都可能增大流量,直到某次dfs找不到可行路径为止,最大流就求出
来了, 这个想法是否正确?
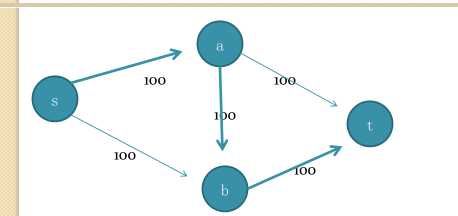
如果我们沿着s-a-b-t路线走 仅能得到一个100的流
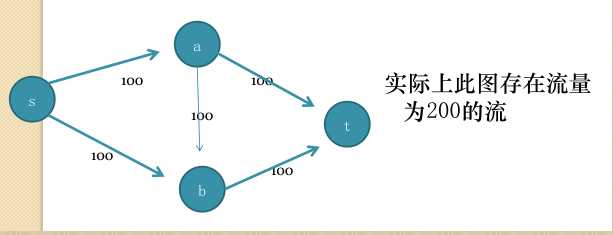
实际上此图存在流量为200的流
问题出在过早地认为边 a → b b 上流量不为0 0 ,因而“封锁”了流量继续增大的可能。
一个改进的思路:应能够修改已建立的流网络,使得“不合理”的流量被删掉。 一种实现:对上次 dfs 时找到的流量路径上的边,添加一条“反向”边,反向边上的容量等于上次 dfs 时找到的该边上的流量,然后再利用“反向”的容量和其他边上剩余的容量寻找路径。
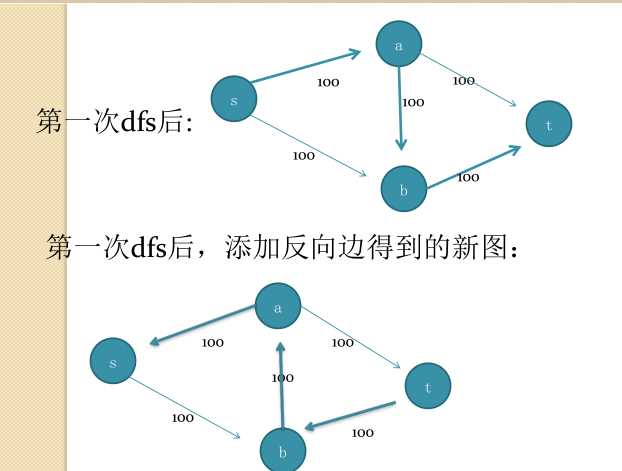
第一次dfs后,添加反向边得到的新图:这样我们第二次dfs搜索的时候就可以在新的网络里找到新的路径这是一个取消流的操作 也可以看作是两条路径的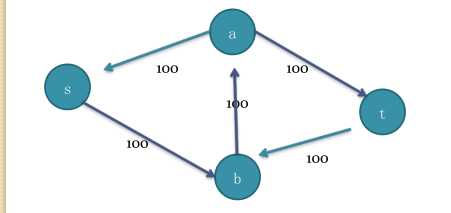
第二次dfs搜索又找到了一个流量为100的流,加上第一次搜索得到的流量为100的流,总流量上升到200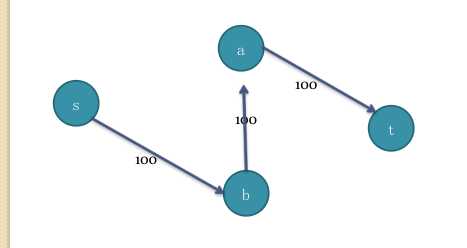
再对第二次dfs后的图添加反向边,
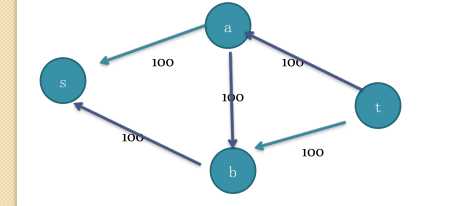
变成:在此图上再次进行dfs,已经找不到路径了,所以流量无法再增加,最大流就是200
残余网络 (ResidualNetwork)
在一个网络流图上,找到一条源到汇的路径(即找到了一个流量)后,对路径上所有的边,其容量都减去此次找到的流量,对路径上所有的边,都添加一条反向边,其容量也等于此次找到的流量,这样得到的新图,就称为原图的“残余网络”为什么添加反向边(取消流)是有效的?假设在第一次寻找流的时候,发现在b->a上可以有流量n来自源,到达b,再流出a后抵达汇点。
为什么添加反向边(取消流)是有效的?构建残余网络时添加反向边a->b,容量是n,增广的时候发现了流量n-k,即新增了n-k的流量。这n-k的流量,从a进,b出,最终流到汇n-k现要证明这2n-k的从流量,在原图上确实是可以从源流到汇的。把流入b的边合并,看做一条,把流出a的边也合并,同理把流入a和流出b的边也都合并。
在原图上可以如下分配流量,则能有2n-k从源流到汇点:
没有严格证明,只给一个感性认识。几条反向边相连的各种复杂情况也可以类似分析。
Ford-Fulkerson算法
? 求最大流的过程,就是不断找到一条源到汇路径,然后构建残余网络,再在残余网络上寻找新的路径,使 总流量增加,然后形成新的残余网络,再寻找新路径 … .. 直到某个残余网络上找不到从源到汇的路径为止,最大流就算出来了。 每次寻找新流量并构造新残余网络的过程,就叫做寻找流量的“增广路径”,也叫“增广”现在假设每条边 的容量都是 整数这个 算法每次都能将流至少增加1由于 整个网络的流量最多不超过 图中所有的边 的容量和C ,从而 算法会 结束现在来看复杂度找增广路径的算法可以用dfs , 复杂度为边数m+ 顶点数nDfs 最多 运行C 次所以时间复杂度为C*(m+n) =C* n^2这个算法实现很简单但是注意到在图中C可能很大很大,比如说下面这张图
如果运气不好 这种图会让你的程序执行200次dfs虽然实际上最少只要2次我们就能得到最大流如何避免上述的情况发生?在每次增广的时候,选择从源到汇的具有最少边数的增广路径,即不是通过dfs寻找增广路径,而是通过bfs寻找增广路径。这就是Edmonds-Karp 最短增广路算法已经证明这种算法的复杂度上限为nm 2 (n是点数,m是边数)
例题:
HDU 1532 http://acm.hdu.edu.cn/showproblem.php?pid=1532
或者 POJ 1273 http://poj.org/problem?id=1273
最大流模版代码

1 #include <cstdio> 2 #include <cstdlib> 3 #include <cstring> 4 #include <cctype> 5 #include <cmath> 6 #include <algorithm> 7 #include <vector> 8 #include <queue> 9 #include <stack> 10 #include <map> 11 using namespace std; 12 13 const int inf = 0x3f; 14 const int INF = 0x3f3f3f3f; 15 const int maxn = 205; 16 int G[maxn][maxn], Prev[maxn]; 17 bool visit[maxn]; 18 queue<int> q; 19 int n, m; 20 21 int Augment(); 22 bool bfs(); 23 24 int main() 25 { 26 int x, y, z; 27 while(~scanf("%d %d", &m, &n)) 28 { 29 memset(G, 0, sizeof(G)); 30 while(m--) 31 { 32 scanf("%d %d %d", &x, &y, &z); 33 G[x][y] += z; 34 } 35 int MaxFlow = 0; 36 int aug; 37 while(bfs())//没有增广路径就找到了最大流 38 MaxFlow += Augment(); 39 printf("%d\n", MaxFlow); 40 } 41 } 42 //用BFS寻找增广路经 43 bool bfs() 44 { 45 while(!q.empty()) q.pop(); 46 int v, i; 47 memset(Prev, 0, sizeof(Prev)); 48 memset(visit, 0, sizeof(visit)); 49 Prev[1] = 0; 50 visit[1] = 1; 51 q.push(1); 52 while(!q.empty()) 53 { 54 v = q.front(); 55 q.pop(); 56 for(int i = 1; i <= n; i++) 57 { 58 if(G[v][i] > 0 && !visit[i]) 59 { 60 Prev[i] = v; visit[i] = 1; 61 if(i == n) 62 { 63 return true; 64 } 65 else 66 { 67 q.push(i); 68 } 69 } 70 } 71 } 72 return false; 73 } 74 // 75 int Augment() 76 { 77 int nMinFlow = INF; 78 int v = n; 79 //这就是刚才用BFS找到的一条增广路径 80 //寻找源到汇的路径上 容量最小的边,其容量就是此次增加的总流量 81 while(Prev[v]) 82 { 83 nMinFlow = min(nMinFlow, G[Prev[v]][v]); 84 v = Prev[v]; 85 } 86 87 v = n; 88 //修该每条边的容量。添加反向边 89 while(Prev[v]) 90 { 91 G[Prev[v]][v] -= nMinFlow; 92 G[v][Prev[v]] += nMinFlow; 93 v = Prev[v]; 94 } 95 return nMinFlow; 96 }
原文:http://www.cnblogs.com/tenlee/p/4456822.html