本文兼参考自《算法导论》及《算法》。
以前一直不能够理解深度优先搜索和广度优先搜索,总是很怕去碰它们,但经过阅读上边提到的两本书,豁然开朗,马上就能理解得更进一步。
在《算法》这本书中,作者写了很好的一个故事。这个故事让我马上理解了深度优先搜索的思想。
如下图1-1所示,如何在这个迷宫中找到出路呢?方法见图1-2.
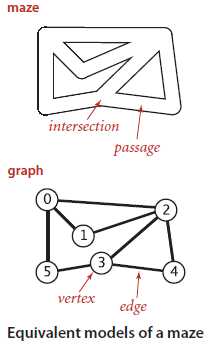
图1-1 等价的迷宫模型
探索迷宫而不迷路的一种古老办法(至少可以追溯到忒修斯和米诺陶的传说)叫做Tremaux搜索,如下图所示。要探索迷宫中的所有通道,我们需要:
1)选择一条没有标记过的通道,在你走过的路上铺一条绳子;
2)标记所有你第一次路过的路口和通道;
3)当来到一个标记过的路口时,用绳子回退到上个路口;
4)当回退到的路口已没有可走的通道时继续回退。
绳子可以保证你总能找到一条出路,标记则能保证你不会两次经过同一条通道或同一个路口。
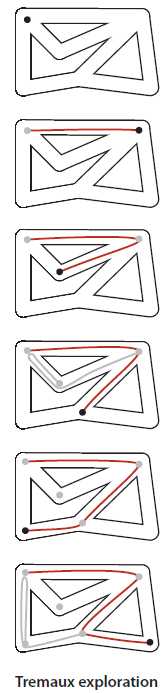
图1-2 Tremaux探索
《算法》作者给出的Java代码如下:

1 public class DepthFirstSearch 2 { 3 private boolean[] marked; 4 private int count; 5 6 public DepthFirstSearch(Graph G, int s) 7 { 8 marked = new boolean[G.V()]; 9 dfs(G, s); 10 } 11 12 private void dfs(Graph G, int v) 13 { 14 marked[v] = true; 15 count++; 16 for(int w : G.adj(v)) 17 { 18 if(!marked[w]) 19 { 20 dfs(G, w); 21 } 22 } 23 } 24 25 public boolean marked(int w) 26 { 27 return marked[w]; 28 } 29 30 public int count() 31 { 32 return count; 33 } 34 }
具体例子如下图1-3:
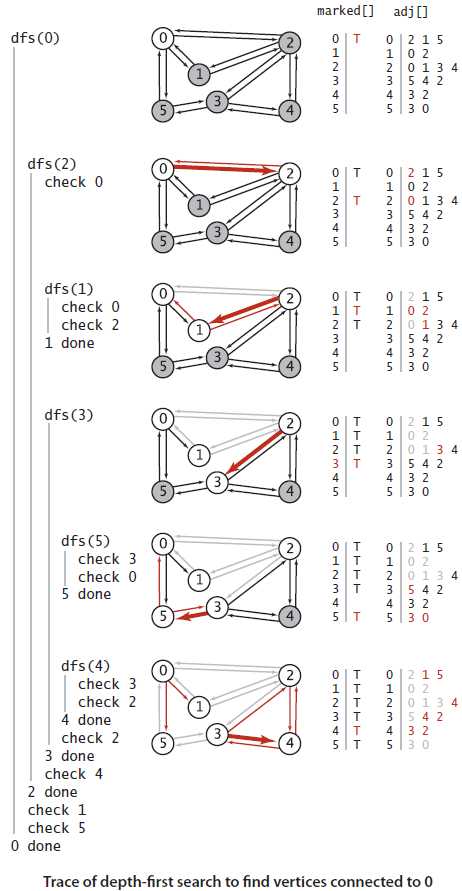
图1-3 使用深度优先探索的轨迹,寻找所有和顶点0连通的顶点
《算法》作者给出的Java代码如下:

1 public class DepthFirstPaths 2 { 3 private boolean[] marked; // Has dfs() been called for this vertex? 4 private int[] edgeTo; // last vertex on known path to this vertex 5 private final int s; // source 6 public DepthFirstPaths(Graph G, int s) 7 { 8 marked = new boolean[G.V()]; 9 edgeTo = new int[G.V()]; 10 this.s = s; 11 dfs(G, s); 12 } 13 14 private void dfs(Graph G, int v) 15 { 16 marked[v] = true; 17 for (int w : G.adj(v)) 18 if (!marked[w]) 19 { 20 edgeTo[w] = v; 21 dfs(G, w); 22 } 23 } 24 25 public boolean hasPathTo(int v) 26 { 27 return marked[v]; 28 } 29 30 public Iterable<Integer> pathTo(int v) 31 { 32 if (!hasPathTo(v)) return null; 33 Stack<Integer> path = new Stack<Integer>(); 34 for (int x = v; x != s; x = edgeTo[x]) 35 path.push(x); 36 path.push(s); 37 return path; 38 } 39 }
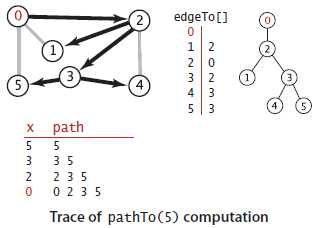
图1-4 pathTo(5)的计算轨迹
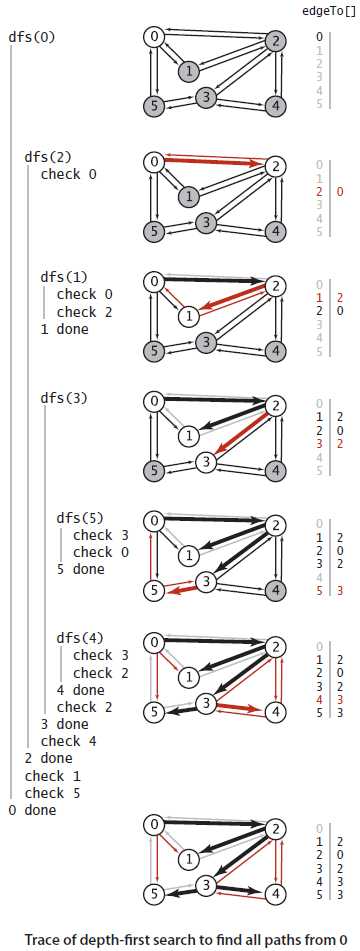
图1-5 使用深度优先搜索的轨迹,寻找所有起点为0的路径
深度优先搜索就好像是一个人在走迷宫,广度优先搜索则好像是一组人在一起朝各个方向走这座迷宫,每个人都有自己的绳子。当出现新的叉路时,可以假设一个探索者可以分裂为更多的人来搜索它们。当两个探索者相遇时,会合二为一(并继续使用先到达者的绳子)。如下图2-1:
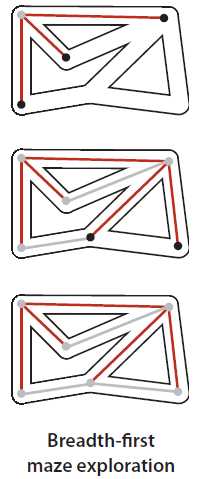
图2-1 广度优先的迷宫搜索
《算法》作者给出的使用广度优先搜索查找图中的路径的Java代码如下:

1 public class BreadthFirstPaths 2 { 3 private boolean[] marked; // Is a shortest path to this vertex known? 4 private int[] edgeTo; // last vertex on known path to this vertex 5 private final int s; // source 6 7 public BreadthFirstPaths(Graph G, int s) 8 { 9 marked = new boolean[G.V()]; 10 edgeTo = new int[G.V()]; 11 this.s = s; 12 bfs(G, s); 13 } 14 15 private void bfs(Graph G, int s) 16 { 17 Queue<Integer> queue = new Queue<Integer>(); 18 marked[s] = true; // Mark the source 19 queue.enqueue(s); // and put it on the queue. 20 while (!q.isEmpty()) 21 { 22 int v = queue.dequeue(); // Remove next vertex from the queue. 23 for (int w : G.adj(v)) 24 if (!marked[w]) // For every unmarked adjacent vertex, 25 { 26 edgeTo[w] = v; // save last edge on a shortest path, 27 marked[w] = true; // mark it because path is known, 28 queue.enqueue(w); // and add it to the queue. 29 } 30 } 31 } 32 33 public boolean hasPathTo(int v) 34 { 35 return marked[v]; 36 } 37 38 public Iterable<Integer> pathTo(int v) 39 // Same as for DFS. 40 }
一个例子如下:
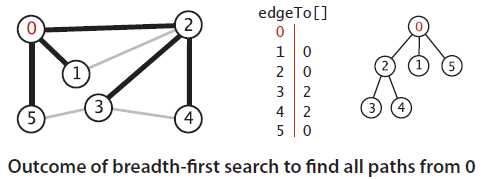
图2-2 使用广度优先搜索寻找所有起点为0的路径的结果
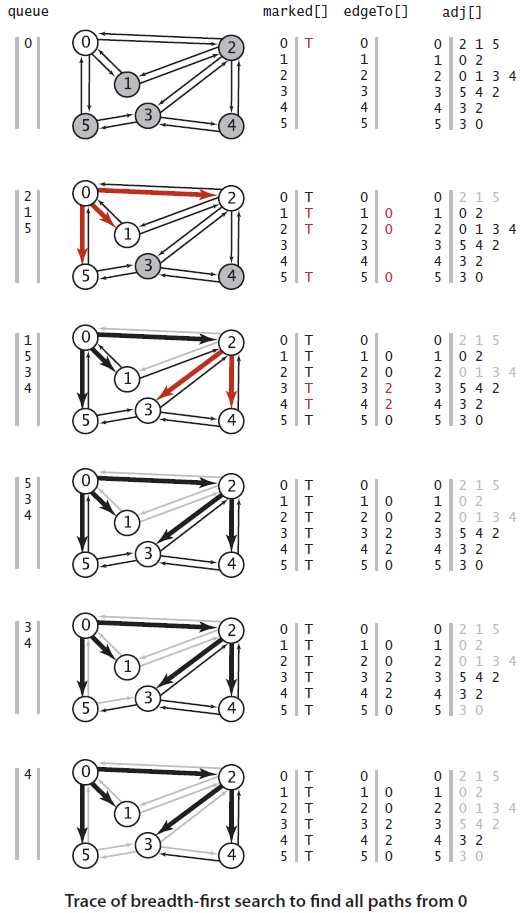
图2-3 使用广度优先搜索的轨迹,寻找所有起点为0的路径
具体代码已经托管到Github.
"《算法导论》之‘图’":深度优先搜索、宽度优先搜索及连通分量
原文:http://www.cnblogs.com/xiehongfeng100/p/4461772.html