Description
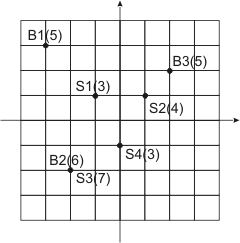 The City has a number of municipal buildings and a number of fallout shelters that were build specially to hide municipal workers in case of a nuclear war. Each fallout shelter has a limited capacity
in terms of a number of people it can accommodate, and there‘s almost no excess capacity in The City‘s fallout shelters. Ideally, all workers from a given municipal building shall run to the nearest fallout shelter. However, this will lead to overcrowding
of some fallout shelters, while others will be half-empty at the same time.
The City has a number of municipal buildings and a number of fallout shelters that were build specially to hide municipal workers in case of a nuclear war. Each fallout shelter has a limited capacity
in terms of a number of people it can accommodate, and there‘s almost no excess capacity in The City‘s fallout shelters. Ideally, all workers from a given municipal building shall run to the nearest fallout shelter. However, this will lead to overcrowding
of some fallout shelters, while others will be half-empty at the same time. Input
Output
Sample Input
3 4 -3 3 5 -2 -2 6 2 2 5 -1 1 3 1 1 4 -2 -2 7 0 -1 3 3 1 1 0 0 0 6 0 0 3 0 2
Sample Output
SUBOPTIMAL 3 0 1 1 0 0 6 0 0 4 0 1
#include<iostream>
#include<cstdio>
#include<cstring>
#include<deque>
#include<cmath>
#include<algorithm>
using namespace std;
const int MAXN = 210;
const int MAXM = 43000;
const int INF = 0x3f3f3f3f;
struct Edge
{
int from, to, cap, next, cost;
};
Edge edge[MAXM];
int head[MAXN];
int prevv[MAXN];
int preve[MAXN];
int has[MAXN];
int senario[MAXN][MAXN];
int dist[MAXN];
int vis[MAXN];
int cntvis[MAXN];
int x[MAXN], y[MAXN], p[MAXN], q[MAXN];
int peo[MAXN], cap[MAXN];
int src, des, cnt;
void addedge( int from, int to, int cap, int cost )
{
edge[cnt].from = from;
edge[cnt].to = to;
edge[cnt].cap = cap;
edge[cnt].cost = cost;
edge[cnt].next = head[from];
head[from] = cnt++;
}
int SPFA( int n )
{
deque<int> dq;
bool inqueue[MAXN];
memset( dist, INF, sizeof dist );
memset( inqueue, 0, sizeof inqueue );
memset( cntvis, 0, sizeof cntvis );
memset( prevv, -1, sizeof prevv );
memset( preve, -1, sizeof preve );
dq.push_back( src );
dist[src] = 0;
inqueue[src] = 1;
cntvis[src]++;
while(!dq.empty( ))
{
int u = dq.front( );
dq.pop_front( );
inqueue[u] = 0;
for(int i = head[u]; i != -1; i = edge[i].next)
{
int v = edge[i].to;
if(edge[i].cap > 0 && dist[u] + edge[i].cost< dist[v])
{
dist[v] = dist[u] + edge[i].cost;
prevv[v] = u;
preve[v] = i;
if(!inqueue[v])
{
inqueue[v] = 1;
cntvis[v]++;
if(cntvis[v] > n) return v;
if(!dq.empty( ) && dist[v] <= dist[dq.front( )])
dq.push_front( v );
else
dq.push_back( v );
}
}
}
}
return -1;
}
void NegaCircle( int ne )
{
memset( vis, 0, sizeof vis );
int st = ne;
while(1)
{
if(!vis[st])
{
vis[st] = 1;
st = prevv[st];
}
else
{
ne = st;
break;
}
}
do
{
int from = prevv[st], to = st; //在负圈上增广
if(from <= 100 && to > 100) senario[from][to - 100]++;
if(from > 100 && to <= 100)senario[to][from - 100]--;
st = prevv[st];
} while(st != ne);
}
int main( )
{
int n, m, f, cost;
while(cin >> n >> m)
{
memset( has, 0, sizeof has );
memset( head, -1, sizeof head );
cnt = 0;
f = 0, cost = 0;
src = 0, des = 205;
for(int i = 1; i <= n; i++)
{
//cin >> x[i] >> y[i] >> peo[i];
scanf( "%d%d%d", &x[i], &y[i], &peo[i] );
}
for(int i = 1; i <= m; i++)
{
//cin >> p[i] >> q[i] >> cap[i];
scanf( "%d%d%d", &p[i], &q[i], &cap[i] );
}
for(int i = 1; i <= n; i++)
{
addedge( src, i, peo[i], 0 );
addedge( i, src, 0, 0 );
}
int trans;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
scanf( "%d", &trans );
senario[i][j] = trans;
has[j] += trans;
int c = abs( x[i] - p[j] ) + abs( y[i] - q[j] ) + 1;
addedge( i, 100 + j, INF - trans, c );
addedge( 100 + j, i, trans, -c );
}
}
for(int i = 1; i <= m; i++)
{
addedge( 100 + i, des, cap[i] - has[i], 0 );
addedge( des, 100 + i, has[i], 0 );
}
int st = SPFA( n + m + 2 );
if(st == -1)
{
printf( "OPTIMAL\n" );
continue;
}
else
{
NegaCircle( st );
printf( "SUBOPTIMAL\n" );
for(int i = 1; i <= n; i++)
{
for(int j = 1; j < m; j++)
{
printf( "%d ", senario[i][j] );
}
printf( "%d\n", senario[i][m] );
}
}
}
return 0;
}
解题报告 之 POJ2175 Evacuation Plan
原文:http://blog.csdn.net/maxichu/article/details/45420165