PRML 1: Gaussian Distribution

1. Overview of Machine Learning

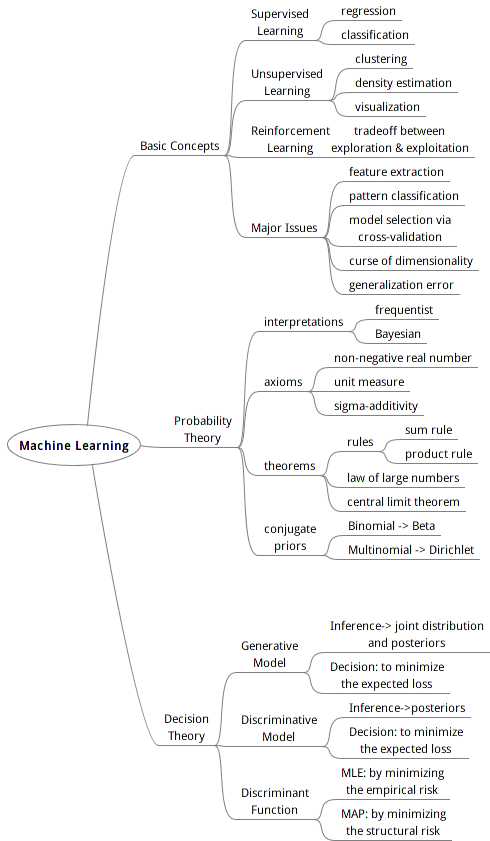
　　The information of a random variable in terms of its distribution can be measured as entropy.

　　The maximum entropy configuration for a discrete variable is the uniform distribution, and for a continuous variable is the Gaussian distribution.

　　The additional amount of information required as we approximate a random variable with another distribution is called relative entropy (KL-divergence).

　　The KL-divergence between the joint distribution and the product of two marginals is called mutual information.

2. The Gaussian Distribution

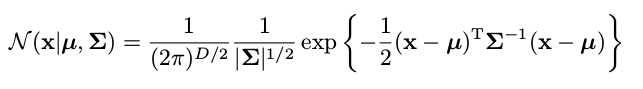
　　Partitioned Gaussians: Suppose x = [x1; x2] obeys the Gaussian distribution with the mean vector mu = [mu1; mu2]

　　　　　　　　　　　　　and the covariance matrix SIG = [SIG11,SIG12; SIG21,SIG22], as well as the precision matrix

　　　　　　　　　　　　　LAMB = [LAMB11,LAMB12; LAMB21, LAMB22] = inv(SIG), then we have:

　　　　　　　(1) Marginal Distribution: p(x1) = Gauss(mu1,SIG11), p(x2) = Gauss(mu2,SIG22) ;

　　　　　　　(2) Conditional Distribution: p(x1|x2) = Gauss(x1-inv(LAMB11)*LAMB12*(x2-mu2), inv(LAMB11)).

　　Linear Gaussian Model: Given p(x) = Gauss(mu,inv(LAMB)) and p(y|x) = Gauss(A*x+b,inv(L)), then we have:

　　　　　　　(1)  p(y) = Gauss(A*mu+b,inv(L)+A*inv(LAMB)*A‘)

　　　　　　　(2)  p(x|y) = Gauss(SIG*{A‘*L*(y-b)+LAMB*mu},SIG), where SIG = inv(LAMB+A‘*L*A).

　　Maximum Likelihood Estimate: The mean vector can be estimated sequentially by mu = mu + (x_cnt - mu) / cnt, whereas

　　　　　　　　　　　　　the covariance matrix can only be obtained by SIG = sum_i((x_i-mu)*(x_i-mu)‘) / cnt.

　　The distribution of parameters can be obtained by Bayeisan Inference so long as we have maintained the sufficient statics.

References:

　　1. Bishop, Christopher M. Pattern Recognition and Machine Learning [M]. Singapore: Springer, 2006

PRML 1: Gaussian Distribution

原文：http://www.cnblogs.com/DevinZ/p/4419433.html