sum[i, j, s] 表示第 i 行第 j 个位置以前(第1到第 i 行,第 i 行第1列到第 j – 1 列)已经全部填满,在状态s的约束下要填满剩余位置的可行方案数。s 是压缩表示的第 i 和第 i + 1 行蛋糕放置状况,sj = (1 << (j - 1)) & s,s 的最低有效位表示第 i 行第1个位置的情况、最高有效位表示第 i + 1 行第 m 个位置的情况,1表示填充了,0表示没有填充。
状态转移方程如下:
(图中第二个状态应该分成两种,若 i = N,则等于1,否则才是图中所示)。
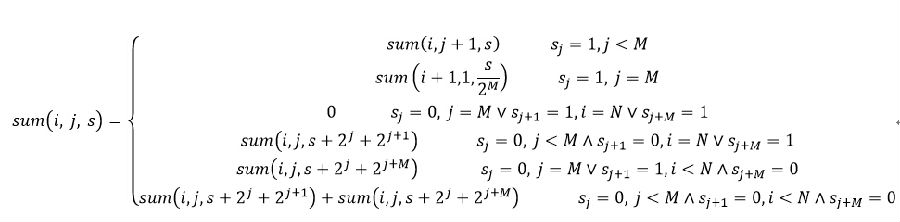
这个方程的分支写的相当复杂,实际上,主要看三个条件:
1. 当前位置 (i, j) 是否已经填充;
2. 当前位置是否有右侧 (i, j + 1),若有,右侧是否已经填充;
3. 若当前位置没填能否填充当前位置及其右侧当前位置是否有下侧 (i + 1, j),若有,下侧是否已经填充。
这三个条件是为了判断是否需要、是否能够填充当前位置,如需要且能填充,如何填充。
最后的结果表示就是 sum[1, 1, 0]。
#include <iostream>
#include <algorithm>
using namespace std;
int sum[1005][6][1 << 10];
int n, m;
int main() {
cin >> n >> m;
for (int i = n; i >= 1; i--) {
for (int j = m; j >= 1; j--) {
for (int k = (1 << (2 * m)) - 1; k >= 0; k--) {
if ((1 << (j - 1)) & k) {
if (j == m) {
if (i < n) {
sum[i][j][k] = sum[i + 1][1][k >> m];
}
else {
sum[i][j][k] = 1;
}
}
else {
sum[i][j][k] = sum[i][j + 1][k];
}
}
else {
bool r_set = ((j == m) || ((1 << (j)) & k));
bool d_set = ((i == n) || ((1 << (j + m - 1)) & k));
if (r_set) {
if (d_set) {
sum[i][j][k] = 0;
}
else {
sum[i][j][k] = sum[i][j][k + (1 << (j - 1)) + (1 << (m + j - 1))];
}
}
else {
if (d_set) {
sum[i][j][k] = sum[i][j][k + (1 << (j - 1)) + (1 << j)];
}
else {
sum[i][j][k] = sum[i][j][k + (1 << (j - 1)) + (1 << (m + j - 1))]
+ sum[i][j][k + (1 << (j - 1)) + (1 << j)];
}
}
}
sum[i][j][k] %= 1000000007;
}
}
}
cout << sum[1][1][0] << endl;
return 0;
}原文:http://www.cnblogs.com/xblade/p/4474875.html