sicp第1章

牛顿迭代法求平方：

(define (sqrt-iter guess x)
  (if (good-enough? guess x)
      guess
      (sqrt-iter (improve guess x) x)
      )
  )
(define (improve guess x)
  (average guess (/ x guess)))
(define (average x y)
  (/ (+ x y) 2))
(define (square x) (* x x))
(define (good-enough? guess x)
  (< (abs (- (square guess) x)) 0.001))

(define (sqrt x)
  (sqrt-iter 1.0 x))

习题1.6：

以下是 Alyssa 的 new-if 定义：

;;; 6-new-if.scm

(define (new-if predicate then-clause else-clause)
    (cond (predicate then-clause)
          (else else-clause)))
把if换成new-if可以吗？

;;; 6-sqrt-iter.scm

(load "6-new-if.scm")

(load "p15-good-enough.scm")                ; 定义平方根用到的其他函数
(load "p15-improve.scm")
(load "p16-sqrt.scm")

(define (sqrt-iter guess x)
    (new-if (good-enough? guess x)          ; <-- new-if 在这里
            guess
            (sqrt-iter (improve guess x)
                        x)))

1 ]=> (load "6-sqrt-iter.scm")

;Loading "6-sqrt-iter.scm"...
;  Loading "6-new-if.scm"... done
;  Loading "p15-good-enough.scm"... done
;  Loading "p15-improve.scm"...
;    Loading "p15-average.scm"... done
;  ... done
;  Loading "p16-sqrt.scm"...
;    Loading "p15-sqrt-iter.scm"...
;      Loading "p15-good-enough.scm"... done
;      Loading "p15-improve.scm"...
;        Loading "p15-average.scm"... done
;      ... done
;    ... done
;  ... done
;... done
;Value: sqrt-iter

1 ]=> (sqrt 9)

;Aborting!: maximum recursion depth exceeded

1 ]=> (trace sqrt-iter)

;Unspecified return value

1 ]=> (sqrt 9)

; ...

[Entering #[compound-procedure 11 sqrt-iter]
    Args: 3.
          9]

[Entering #[compound-procedure 11 sqrt-iter]
    Args: 3.
          9]

[Entering #[compound-procedure 11 sqrt-iter]
    Args: 3.
          9]

; ...

[Entering #[compound-procedure 11 sqrt-iter]
    Args: 3.
          9]
^Z
[1]+  已停止               mit-scheme

1 ]=> (if #t (display "good") (display "bad"))
good
;Unspecified return value

1 ]=> (new-if #t (display "good") (display "bad"))
badgood
;Unspecified return value

(define (sqrt-iter guess x)
    (new-if (good-enough? guess x)          ; <- sqrt-iter 的返回值还要作为 new-if 的参数，因此 sqrt-iter 的调用不是尾递归
            guess
            (sqrt-iter (improve guess x)    ; <- 无论 good-enough? 的结果如何
                       x)))                 ;    这个函数调用都会被一直执行下去

书里给了一个树形递归的解法，思路非常简单，把所有的换法分成两类，包含50美分的和不包含的。包含50美分的换法里，因为它至少包含一张50美分，所以它的换法就相当于用5种硬币兑换剩下的50美分的换法；不包含50美分的，只能用4种硬币兑换1美元。这样用5种硬币兑换1美元就等价于用5种硬币兑换50美分的换法加上用前4种硬币兑换1美元的换法。以次类推，用4种硬币兑换1美元的换法就等价于用4种硬币兑换75美分的换法加上用3种硬币兑换1美元的换法。

假设用1种硬币求换法数量的函数是f(n)，用2种的是g(n)，3种的是h(n)，4种的是i(n)，5种的是j(n)，那么

j(100) = j(50) + i(100)
j(50) = j(0) + i(50)
j(0) = 1 #有1种兑法兑换0元，那就是一个硬币都没有

i(100) = i(75) + h(100)
i(75) = i(50) + h(75)
i(50) = i(25) + h(50)
i(25) = i(0) + h(25)
i(0) = 1

;求兑换零钱方式
(define (cc amount kinds-of-coins)
  (cond 
    [(= amount 0) 1]
    [(or (< amount 0) (= kinds-of-coins 0)) 0]
    [else (+ (cc amount (- kinds-of-coins 1))
             (cc (- amount (first-denomination kinds-of-coins)) kinds-of-coins))
             
          ]
    )
  )


(define (first-denomination kinds-of-coins)
  (cond [(= kinds-of-coins 1) 1]
        [(= kinds-of-coins 2) 5]
        [(= kinds-of-coins 3) 10]
        [(= kinds-of-coins 4) 25]
        [(= kinds-of-coins 5) 50]))

(define (count-change amount)
  (cc amount 5)
  )
(count-change 100)

http://blog.pengqi.me/2012/06/07/sicp-making-change/

1. 用了最大的面额的，减去最大面额的值，递归。
2. 没有用最大面额兑换的，不考虑最大的面额，递归。

然后这样就会展开一个二叉树，其中树叶的数量就是总数，可以画图来看一下：

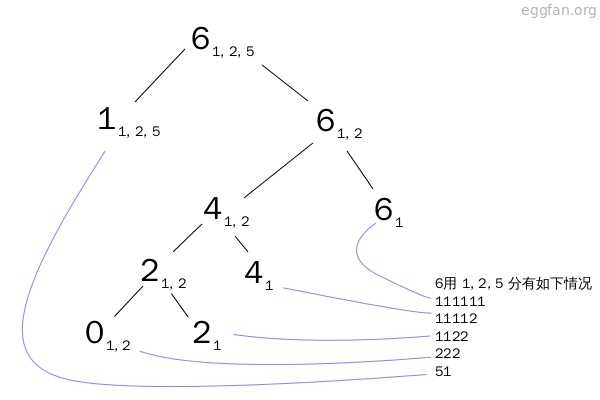
这张图是用这样的方法，用1, 2, 5 去划分 6的情况。每个节点的左枝是第一种方法所递归的，右枝是第二种。(update: 之前这里左右搞反了。)

然后蓝色的线就代表每个叶子所对应的排列方式。

迭代：

n = 30
v = [1,  5, 10, 25, 50]
L = [i==0 for i in range(n+1)]

for i in range(len(v)):
    for j in xrange(v[i], len(L)):
        L[j] += L[j - v[i]]
print L[n]

参考：http://www.zhihu.com/question/22219036、

Exercise 1.11.  A function f is defined by the rule that f(n) = n if n<3 and f(n) = f(n - 1) + 2f(n - 2) + 3f(n - 3) if n> 3. Write a procedure that computes f by means of a recursive process. Write a procedure that computes f by means of an iterative process.

迭代还不太清楚怎么写，

要写出函数 f 的迭代版本，关键是在于看清初始条件和之后的计算进展之间的关系，就像书本 25-26 页中，将斐波那契函数从递归改成迭代那样。

根据函数 f 的初始条件『如果 n<3 ，那么 f(n)=n 』，有等式：

f(0)=0

f(1)=1

f(2)=2

另一方面， 根据条件『当 n≥3 时，有 f(n)=f(n?1)+2f(n?2)+3f(n?3) 』，如果继续计算下去，一个有趣的结果就会显现出来：

f(3)=f(2)+2f(1)+3f(0)

f(4)=f(3)+2f(2)+3f(1)

f(5)=f(4)+2f(3)+3f(2)

…

可以看出，当 n≥3 时，所有函数 f 的计算结果都可以用比当前 n 更小的三个 f 调用计算出来。

迭代版的函数定义如下：它使用 i 作为渐进下标， n 作为最大下标， a 、 b 和 c 三个变量分别代表函数调用 f(i+2) 、 f(i+1) 和 f(i) ，从 f(0) 开始，一步步计算出 f(n) ：

;; 11-iter.scm

(define (f n)
    (f-iter 2 1 0 0 n))

(define (f-iter a b c i n)
    (if (= i n)
        c
        (f-iter (+ a (* 2 b) (* 3 c))   ; new a
                a                       ; new b
                b                       ; new c
                (+ i 1)
                n)))

两个 f 函数不仅使用的计算方式不同（前一个递归计算，另一个迭代计算），而且效率方面也有很大的不同。

递归版本的函数 f 有很多多余的计算，比如说，要计算 f(5) 就得计算 f(4) 、 f(3) 和 f(2) ，而计算 f(4) 又要计算 f(3) 、 f(2) 和 f(1) 。

对于每个 f(n) 调用，递归版 f 函数都要执行 f(n?1) 、 f(n?2) 和 f(n?3) ，而 f(n?1) 的计算又重复了对 f(n?2) 和 f(n?3) 的计算，因此，递归版本的 f 函数是一个指数级复杂度的算法（和递归版本的斐波那契数函数类似）。

另一方面，迭代版本使用三个变量储存 f(n?1) 、 f(n?2) 和 f(n?3) 的值，使用自底向上的计算方式进行计算，因此迭代版的函数 f 没有多余的重复计算工作，它的复杂度正比于 n ，是一个线性迭代函数。

row:
0        1
1       1 1
2      1 2 1
3     1 3 3 1
4    1 4 6 4 1
5   . . . . . .
col: 0 1 2 3 4

;;; 12-rec-pascal.scm

(define (pascal row col)
    (cond ((> col row)
            (error "unvalid col value"))
          ((or (= col 0) (= row col))
            1)
          (else (+ (pascal (- row 1) (- col 1))
                   (pascal (- row 1) col)))))

sicp第1章,布布扣,bubuko.com

sicp第1章

原文：http://www.cnblogs.com/youxin/p/3601291.html