10790 How Many Points of Intersection?

数学题

推导过程：

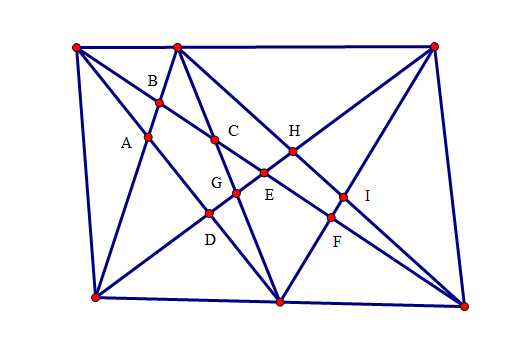
（a-1）个点与a的第一个点与b个点相连的线的交点的个数为：

(a-1)[(b-1)+(b-2)+(b-3)+...+2+1]

（a-2）个点与a的第二个点与b个点相连的线的交点的个数为：

(a-2)[(b-1)+(b-2)+(b-3)+...+2+1]

...

（a-（a-1））个点与a的第（a-1）个点与b个点相连的线的交点的个数为：

1*[(b-1)+(b-2)+(b-3)+...+2+1]

累加得，

[(a-1)+(a-2)+(a-3)+...+2+1]*[(b-1)+(b-2)+(b-3)+...+2+1]。

所以所求相交点的个数为：a*(a-1)*b*(b-1)/4。

 1 #include<stdio.h>
 2 int main()
 3 {
 4     long long a, b,count=1;
 5     while (scanf("%lld%lld", &a, &b))
 6     {
 7         if (a == 0 && b == 0)
 8             break;
 9         printf("Case %lld: ", count);
10         printf("%lld\n",a*(a-1)*b*(b-1)/4);
11         ++count;
12     }
13 }

总结：一开始只知道有这个公式，在东阳的帮助下，知道了怎么推导，很开心！

10790 How Many Points of Intersection?

原文：http://www.cnblogs.com/longzu/p/4480997.html