假设Ax=b,对于矩阵A,以column picture视角看,每一个x,都是A的列的一种线性组合,每种组合均构成一个b。取遍x 得到的所有的b 构成了A的column space
假设Ax=0,所有的解x构成的空间就是A的nullspace.
如果A可逆,那么A的nullspace只包含零向量;否则A的nullspace包含一系列的解(不可能无解,因为x=0永远都是解)。
假设Ax=0,对A进行elimination不会影响方程组的解,所以elimination之后的A和原先的A有共同的nullspace(但是他们的column space不同)。
高斯消元法将A转化成一个上“梯形”矩阵U,U还能进一步转化成R(=reduced):pivot均为1,且pivot上下都是0. pivot所在的列对应的x分量是pivot variable,其余是free variable,例如下图的R,x1和x3是pivot variable,x2是free variable.
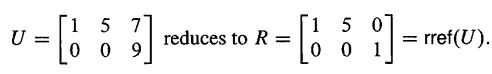
化成R的好处是:Ax=0的解可以方便看出。注意,Ax是A各个列的线性组合,而R中free column 可以很容易地用pivot column表示出来(将pivot column组合起来就是I),如上例:col2 = 5 * col1 + 0 * col3
取x2=1,得到方程的解是x=c*[-5,1, -0]T,c是一个常数,(-5,0)=(x2在R中对应的列)*-1
再如:
\( R=rref(A)=\begin{bmatrix}\mathbf{1} & 1 & \mathbf{0} & 1\\ \mathbf{0} & 0 & \mathbf{1} & 1\\ 0 & 0 & 0 & 0\end{bmatrix} \)
第一步令(x2,x4)=(1,0),第二步令(x2,x4)=(0,1),对应的解是:
\( x=x_2\begin{bmatrix}-1\\ \mathbf{1}\\ 0\\ \mathbf{0}\end{bmatrix}+x_4\begin{bmatrix}-1\\\mathbf{0}\\-1\\\mathbf{1} \end{bmatrix} \)
假设\( R= \begin{bmatrix} I & F \end{bmatrix} \),那么R对应的nullspace matrix就是\( X=\begin{bmatrix} -F \\ I \end{bmatrix} \)
原文:http://www.cnblogs.com/ericxing/p/3607530.html