单精度浮点数按存储格式转为整数的程序

///////////////////
#include<cstdio>

//-----------------
union int_char
{
    unsigned char ch[4];
    float i;
};

void out_put(union int_char x)//x86是小端对其模式，即最数据的最低位存储在地址的最低位上。
{
    printf("单精度浮点数值为：%f\n",x.i,x.i);
    printf("存储位置从左到右，从高位到低位依次为 0x：\n");
    printf("%X ",x.ch[3]);//最高位
    printf("%X ",x.ch[2]);
    printf("%X ",x.ch[1]);
    printf("%X \n\n",x.ch[0]);//最低位

}

//----------------

int main(int argc, char* argv[])
{

    union int_char x;
    //x.i=123.456;
    //x.i=1.0;
    x.i=3.0;
    out_put(x);


    system("pause");
    return 0;
}

单精度浮点数

1.IEEE 754 标准所定义的单精度浮点数的长度为 32 位，按位域可划分为：符号位、阶码位与尾数位，如下：

  31----------------------22---------------------------------------------------------0
  |                       |                                                          |
  X X X X    X X X X    X X X X    X X X X    X X X X    X X X X    X X X X    X X X X
  | |-------------------| |----------------------------------------------------------|
符号        阶码                                     尾数

符号位取 0 表示正数，取 1 表示负数。

阶码位是 8 位，这里有一点小门道需要注意，那就是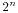的指数 n 并不能直接当作阶码来处理，需要将其与 127 (0x7f) 相加才可得到  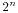的阶码表示。

尾数的位域长度在图示中是 23 位，但实际上却是 24 位，这个位是“不可见”的，其值固定为 1，这也就是说 IEEE 754 标准所定义的浮点数，其有效数字是介于 1 与 2 之间的小数。

可以尝试写一下 1.0 这个数的二进制单精度浮点格式，这有助于更好地理解单精度浮点数格式的位域分布。

1.0 的二进制单精度浮点格式：0 0111 1111 000 0000 0000 0000 0000 0000

值得注意的一个问题是：书上说之所以要将指数加上 127 来得到阶码，是为了简化浮点数的比较运算，这一点我没有体会出来。但是通过 127 这个偏移量 (移码)，可以区分出指数的正负。阶码为 127 时表示指数为 0；阶码小于 127 时表示负指数；阶码大于 127 时表示正指数。

2.首先将十进制数123.456转换为二进制数为：1111011. 01110100101111001 

      （其中0.456如何转换为二进制？不断乘2取整，顺序排列

       如:0.734375转二进制，结果是101111。

          0.734375 x 2 = 1.46875 
          0.46875 x 2 = 0.9375 
          0.9375 x 2 = 1.875 
          0.875 x 2 = 1.75 
          0.75 x 2 = 1.5 
          0.5 x 2 = 1.0） 

      1111011. 01110100101111001 即1. 11101101110100101111001乘以2的6次方

      首先这是一个正数，则符号位为0

      阶码为6，不过要转换成移码。

      （如何求6的移码？这里我也不太深究，我见大家都是直接6+127=133，换为2进制为10000101）

      （移码与补码的关系： [X]移与[X]补的关系是符号位互为相反数（仅符号位不同））

      尾数则为1. 11101101110100101111001的小数部分，即

11101101110100101111001

综上：123.456的二进制存储格式为：01000010111101101110100101111001

代码运行结果如下：

浮点数：1.0   (0 0111 1111 000 0000 0000 0000 0000 0000）

从高位到低位依次是：单精度浮点数值为：1.000000
存储位置从左到右，从高位到低位依次为 0x：
3F 80 0 0

=======================

浮点数：123.456  （01000010111101101110100101111001）

单精度浮点数值为：123.456001
存储位置从左到右，从高位到低位依次为 0x：
42 F6 E9 79


请按任意键继续. . .

用下面的代码也可以实现:

    float i=3.0;
    unsigned char* p=(unsigned char *)&i;


    printf("单精度浮点数值为：%f\n",i);
    printf("存储位置从左到右，从高位到低位依次为 0x：\n");
    printf("%X ",*(p+3));
    printf("%X ",*(p+2));
    printf("%X ",*(p+1));
    printf("%X \n\n",*p);

得到的结果是相同的。

单精度浮点数按存储格式转为整数的程序

原文：http://blog.csdn.net/u013467442/article/details/46316641