
改革春风吹满地 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 16889 Accepted Submission(s): 8636 Problem Description “ 改革春风吹满地, 不会AC没关系; 实在不行回老家, 还有一亩三分地。 谢谢!(乐队奏乐)” 话说部分学生心态极好,每天就知道游戏,这次考试如此简单的题目,也是云里雾里,而且,还竟然来这么几句打油诗。 好呀,老师的责任就是帮你解决问题,既然想种田,那就分你一块。 这块田位于浙江省温州市苍南县灵溪镇林家铺子村,多边形形状的一块地,原本是linle 的,现在就准备送给你了。不过,任何事情都没有那么简单,你必须首先告诉我这块地到底有多少面积,如果回答正确才能真正得到这块地。 发愁了吧?就是要让你知道,种地也是需要AC知识的!以后还是好好练吧... Input 输入数据包含多个测试实例,每个测试实例占一行,每行的开始是一个整数n(3<=n<=100),它表示多边形的边数(当然也是顶点数),然后是按照逆时针顺序给出的n个顶点的坐标(x1, y1, x2, y2... xn, yn),为了简化问题,这里的所有坐标都用整数表示。 输入数据中所有的整数都在32位整数范围内,n=0表示数据的结束,不做处理。 Output 对于每个测试实例,请输出对应的多边形面积,结果精确到小数点后一位小数。 每个实例的输出占一行。 Sample Input 3 0 0 1 0 0 1 4 1 0 0 1 -1 0 0 -1 0 Sample Output 0.5 2.0
有关叉积相关:http://www.cnblogs.com/wushuaiyi/p/3458659.html

1 #include <stdio.h> 2 3 struct node{ 4 double x,y; 5 }a[110],p1,p2; 6 7 int main(){ 8 int i,j,t; 9 double ans; 10 while(scanf("%d",&t)!=EOF){ 11 if(t == 0) 12 break; 13 ans = 0.00000; 14 for(i=0;i<t;i++) 15 scanf("%lf%lf",&a[i].x,&a[i].y); 16 for(i=0;i<t-1;i++){ 17 ans += ((a[i].x * a[i+1].y) - (a[i+1].x * a[i].y))/2; 18 } 19 ans+=((a[t-1].x * a[0].y) - (a[0].x * a[t-1].y))/2; 20 printf("%.1lf\n",ans); 21 } 22 return 0; 23 }

Lifting the Stone Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 4898 Accepted Submission(s): 2038 Problem Description There are many secret openings in the floor which are covered by a big heavy stone. When the stone is lifted up, a special mechanism detects this and activates poisoned arrows that are shot near the opening. The only possibility is to lift the stone very slowly and carefully. The ACM team must connect a rope to the stone and then lift it using a pulley. Moreover, the stone must be lifted all at once; no side can rise before another. So it is very important to find the centre of gravity and connect the rope exactly to that point. The stone has a polygonal shape and its height is the same throughout the whole polygonal area. Your task is to find the centre of gravity for the given polygon. Input The input consists of T test cases. The number of them (T) is given on the first line of the input file. Each test case begins with a line containing a single integer N (3 <= N <= 1000000) indicating the number of points that form the polygon. This is followed by N lines, each containing two integers Xi and Yi (|Xi|, |Yi| <= 20000). These numbers are the coordinates of the i-th point. When we connect the points in the given order, we get a polygon. You may assume that the edges never touch each other (except the neighboring ones) and that they never cross. The area of the polygon is never zero, i.e. it cannot collapse into a single line. Output Print exactly one line for each test case. The line should contain exactly two numbers separated by one space. These numbers are the coordinates of the centre of gravity. Round the coordinates to the nearest number with exactly two digits after the decimal point (0.005 rounds up to 0.01). Note that the centre of gravity may be outside the polygon, if its shape is not convex. If there is such a case in the input data, print the centre anyway. Sample Input 2 4 5 0 0 5 -5 0 0 -5 4 1 1 11 1 11 11 1 11 Sample Output 0.00 0.00 6.00 6.00
求任意多边形的重心(from:http://www.cnblogs.com/bo-tao/archive/2011/08/16/2141395.html)
已知一多边形没有边相交,质量分布均匀。顺序给出多边形的顶点坐标,求其重心。
分析:
求多边形重心的题目大致有这么几种:
1,质量集中在顶点上。n个顶点坐标为(xi,yi),质量为mi,则重心
X = ∑( xi×mi ) / ∑mi
Y = ∑(
yi×mi ) / ∑mi
特殊地,若每个点的质量相同,则
X = ∑xi / n
Y = ∑yi / n
2,质量分布均匀。这个题就是这一类型,算法和上面的不同。
特殊地,质量均匀的三角形重心:
X = ( x0 + x1 + x2 ) /
3
Y = ( y0 + y1 + y2 ) / 3
3,质量分布不均匀。只能用积分来算,不会……
求任意多边形的重心
已知一多边形没有边相交,质量分布均匀。顺序给出多边形的顶点坐标,求其重心。
分析:
求多边形重心的题目大致有这么几种:
1,质量集中在顶点上。n个顶点坐标为(xi,yi),质量为mi,则重心
X = ∑( xi×mi ) / ∑mi
Y = ∑(
yi×mi ) / ∑mi
特殊地,若每个点的质量相同,则
X = ∑xi / n
Y = ∑yi / n
2,质量分布均匀。这个题就是这一类型,算法和上面的不同。
特殊地,质量均匀的三角形重心:
X = ( x0 + x1 + x2 ) /
3
Y = ( y0 + y1 + y2 ) / 3
3,质量分布不均匀。只能用积分来算,不会……
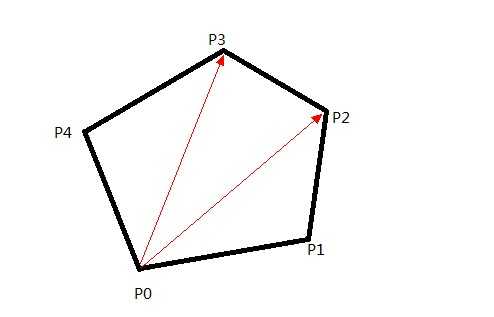
2.7.2 猜想n边形的重心
猜想由n个点(x1,y1), (x2,y2), ……, (xn,yn)
构成的多边形的重心的坐标是:( ( x1+x2...+xn )/n,( y1+y2+...+yn )/n );

1 #include<stdio.h> 2 #include<stdlib.h> 3 int main(){ 4 double x0,y0,x1,y1,x2,y2; 5 int n,m; 6 while(scanf("%d",&n)!=EOF){ 7 for(int i=1; i<=n; i++){ 8 double sx,sy,s; 9 sx = sy = s =0.00000; 10 scanf("%d",&m); 11 scanf("%lf%lf%lf%lf",&x0,&y0,&x1,&y1); 12 for(int j=2;j<m; j++){ 13 scanf("%lf%lf",&x2,&y2); 14 double area=0.50000*((x1-x0)*(y2-y0)-(x2-x0)*(y1-y0)); 15 sx+=area*(x0+x1+x2);//wait to divilded 3 16 sy+=area*(y0+y1+y2); 17 s+=area; 18 x1=x2; 19 y1=y2; 20 } 21 printf("%.2lf %.2lf\n",sx/(3*s),sy/(3*s)); 22 } 23 } 24 return 0; 25 }

You can Solve a Geometry Problem too Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 6551 Accepted Submission(s): 3159 Problem Description Many geometry(几何)problems were designed in the ACM/ICPC. And now, I also prepare a geometry problem for this final exam. According to the experience of many ACMers, geometry problems are always much trouble, but this problem is very easy, after all we are now attending an exam, not a contest :) Give you N (1<=N<=100) segments(线段), please output the number of all intersections(交点). You should count repeatedly if M (M>2) segments intersect at the same point. Note: You can assume that two segments would not intersect at more than one point. Input Input contains multiple test cases. Each test case contains a integer N (1=N<=100) in a line first, and then N lines follow. Each line describes one segment with four float values x1, y1, x2, y2 which are coordinates of the segment’s ending. A test case starting with 0 terminates the input and this test case is not to be processed. Output For each case, print the number of intersections, and one line one case. Sample Input 2 0.00 0.00 1.00 1.00 0.00 1.00 1.00 0.00 3 0.00 0.00 1.00 1.00 0.00 1.00 1.00 0.000 0.00 0.00 1.00 0.00 0 Sample Output 1 3
http://blog.sina.com.cn/s/blog_818d3d930100wpft.html
http://www.cnblogs.com/timeship/archive/2012/08/15/2640801.html
【集训笔记】计算几何【HDOJ2036【HDOJ1086【HDOJ1115,布布扣,bubuko.com
【集训笔记】计算几何【HDOJ2036【HDOJ1086【HDOJ1115
原文:http://www.cnblogs.com/wushuaiyi/p/3612498.html