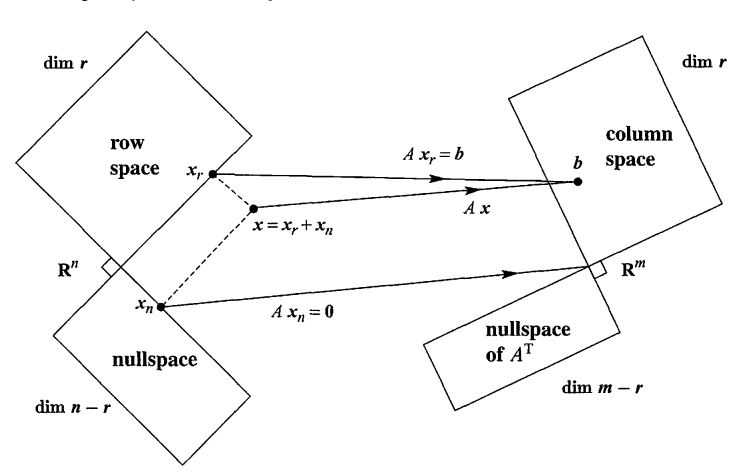
矩阵A的四个子空间是:row space, column space, nullspace and left nullspace,其中:
SPACEA 和 SPACEB 是orthogonal complements的意思是:SPACEA中的任意向量 都和 SPACEB中的任意向量垂直(orthogonal),且dim(SPACEA) + dim(SPACEB) = n,所有与SPACEB垂直的向量都在SPACEA中(complement)
三维空间中,只有:①点 和 整个三维空间;②线 和 垂直于线的平面 才能是orthogonal complements,线和线即使垂直也不是,因为不满足complement这个条件!面和面更不行,orthogonal和complement都不满足!
complement的意义是:任意一个x都能唯一地分为一个row space component xr 和一个nullspace component xn,Ax = Axr+Axn,如图所示:
(并不是所有的b都在column space中,假如Ax=b无解时,b就不是A的column的线性组合,b也就不再A的column space中了。)
寻找向量b在矩阵A构成的column space的投影=Ax
^
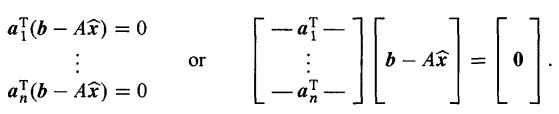
写成:T
(b?Ax
^
)=0
得到:^
=(A
T
A)
?1
A
T
b
=Ax
^
=A(A
T
A)
?1
A
T
b
T
A)
?1
A
T
原文:http://www.cnblogs.com/ericxing/p/3615406.html