小panpan不会图论,所以图论专题他非常刻苦地学习图论。
今天他认真地学习了萌神的ppt,学习了一下Floyd算法,手持两把锟斤拷的他, 口中疾呼烫烫烫,马上找了到OJ上找了道FLoyd的题:
n个点,m边的无向连通图,无重边,无自环,每条边的长度都是1,求任意两点之间的最短距离
—— 出题人acerlawson
小panpan想了想,写了段代码交了上去,他得到了AC!
出题人acerlawson看了一下小panpan的程序,发现他写了个错误的Floyd, 他选了k个点出来,存在a[]数组里,核心代码如下:
d[i][j] // i,j之间的最短距离
a[i] // 小panpan事先选好的点
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == j)
d[i][j] = 0;
else
d[i][j] = INF;
}
}
for (int i = 1; i <= m; i++) {
scanf("%d%d", &u, &v);
d[u][v] = 1;
d[v][u] = 1;
}
for (int r = 1; r <= k; r++) {
v = a[r];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
d[i][j] = min(d[i][j], d[i][v] + d[v][j]);
}
因为数据太水了,所以小panpan得到了AC。 为了让小panpanWA掉,acerlawson想要出一组数据卡掉小panpan的代码,但是acerlawson忙于陪妹子,所以他找你帮忙。
给出一个n个点m条边的无重边无自环的无向连通图,让小panpan的代码得到Wrong Answer。
第一行为三个整数n,m,k(3≤n≤400,n−1≤m≤n(n−1)2,2≤k≤n),分别表示图的顶点数,边数和小panpan选的点的数量
第二行k个整数x1,x2,...,xk,(1≤xi≤n),表示小panpan选的点
输出m行,每行两个整数u和v,表示一条无向边(u,v)
如果有多个解,输出任意可行解
如果无论如何小panpan都能AC,则输出No
| Sample Input | Sample Output |
|---|---|
4 3 2 1 2 |
1 3 2 3 2 4 |
4 3 4 1 2 3 4 |
No |
解题思路:
这是一道构造题.
PPT上那种情况是我们构造的关键.
即我们放一个选择的点在最右边,它的左边一个没有被选的点,再左边整成一个稠密图,容易证明最多支持的边数是:
(n-1)*(n-2) / 2 + x ( x 为没选的点的数量)
图:
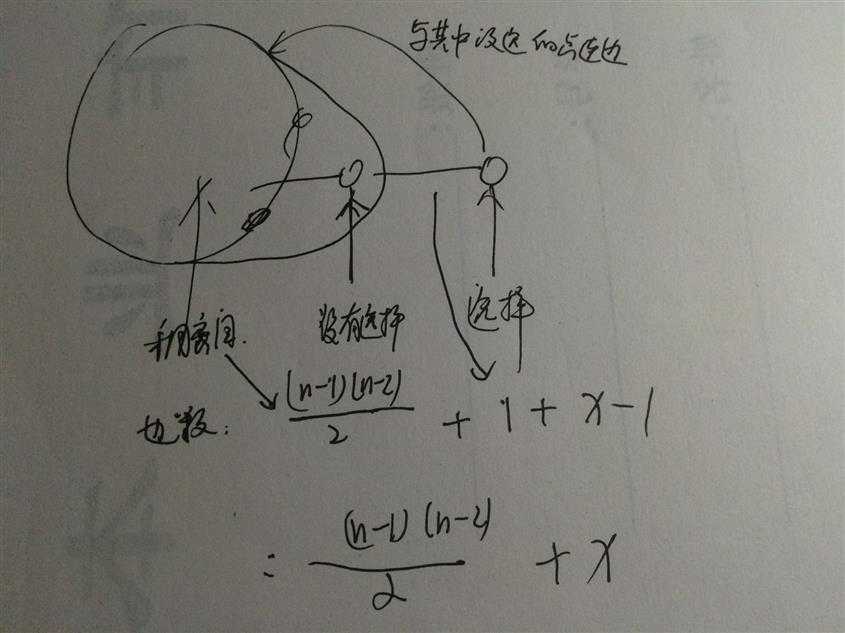
这样,我们就按照这种方法构造即可,注意到如果选了所有点,是构造不出来WA的图的,这点要注意
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> using namespace std; typedef pair <int ,int > Edge; vector<int>s1; //除掉q1,q2的集合 int q1,q2; vector<int>s2; //没有选的点集合 vector<Edge>ans; bool use[450]; //maxedgenumber = (n-1)*(n-2) / 2 + n - k int main(int argc,char *argv[]) { int n,m,k; cin >> n >> m >> k; if (k == n || 2*m > (n-1)*(n-2) + 2*n - 2 *k) cout << "No" << endl; else { memset(use,false,sizeof(use)); int temp1; int ok = 1; for(int i = 0 ; i < k ; ++ i) { int u; cin >> u; use[u] = true; temp1 = u; } q2 = temp1; for(int i = 1 ; i <= n ; ++ i) if(!use[i]) { q1 = i; break; } for(int i = 1 ; i <= n ; ++ i) if (!use[i] && i != q1) s2.push_back(i); for(int i = 1 ; i <= n ; ++ i ) if(i != q1 && i != q2) s1.push_back(i); int tot = 0; for(int i = 0 ; i < s1.size() - 1 ; ++ i) { ans.push_back(Edge(s1[i],s1[i+1])); tot++; } ans.push_back(Edge(s1[s1.size()-1],q1)); ans.push_back(Edge(q1,q2)); tot += 2; for(int i = 0 ; i < s1.size() ; ++ i) for(int j = i + 2 ; j < s1.size() ; ++ j) { if (tot < m) { ans.push_back(Edge(s1[i],s1[j])); tot++; } } int ptr = 0; while(tot < m) { if (ptr >= s1.size() - 1) break; ans.push_back(Edge(s1[ptr++],q1)); tot++; } ptr = 0; while(tot < m) { if (ptr == s2.size()) { ok = 0; break; } if (s2[ptr] == q1) { ptr++; continue; } tot++; ans.push_back(Edge(s2[ptr++],q2)); } if (!ok) printf("No\n"); else { for(int i = 0 ; i < ans.size() ; ++ i) printf("%d %d\n",ans[i].first,ans[i].second); } } return 0; }
UESTC_小panpan学图论 2015 UESTC Training for Graph Theory<Problem J>
原文:http://www.cnblogs.com/Xiper/p/4570666.html