已知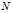
维随机向量
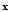服从均值为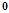
协方差矩阵为
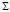的高斯分布：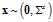
经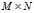
观测矩阵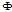
线性变换后得到
维观测向量
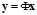，求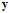
的高斯分布参数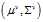
求解过程：令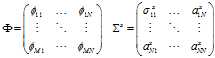 
令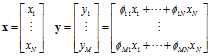 
均值很容易得到：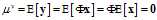
下面详细证明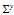
如何得到，先给出结论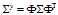
证明：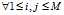
，根据协方差公式有：
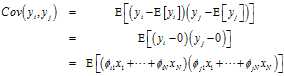
各项进一步展开相乘得到：
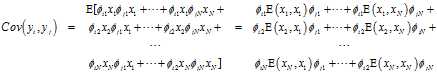
根据已知条件可知：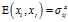
则: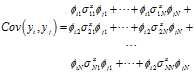
根据下图矩阵中元素的对应关系可以得到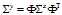
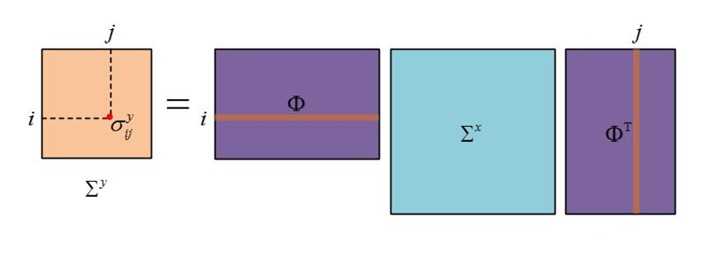所以
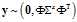
服从正太分布的随机向量经线性变换后的协方差矩阵,布布扣,bubuko.com
原文：http://www.cnblogs.com/brains/p/3617771.html