设计思路:
mport java.awt.Point;
import java.util.Scanner;
public class main {
public static int add(int a[][],int i,int j,int k)
{
int n;
int b=0;
for(n=j;n<=i+j;n++)
{
b+=a[n][k];
}
return b;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
int i,j,k,l;
int sum=0,s,h,e;
Point head=new Point();
Point end=new Point();
Scanner sc=new Scanner(System.in);
System.out.print("请输入矩阵的行数:");
int x=sc.nextInt();
System.out.print("请输入矩阵的列数:");
int y=sc.nextInt();
int a[][]=new int[x][y];
int b[]=new int[y];
System.out.println("请输入数组中的数:");
for(i=0;i<x;i++)
{
for(j=0;j<y;j++)
{
a[i][j]=sc.nextInt();
}
}
for(i=0;i<x;i++)
{
for(j=0;i+j<x;j++)
{
s=0;
h=0;
e=0;
for(k=0;k<y;k++)
{
b[k]=add(a,i,j,k);
}
for(l=0;l<x;l++)
{
s+=b[l];
if(s>0)
{
e++;
}
else
{
s=0;
h=l+1;
e++;
}
if(s>sum)
{
sum=s;
head.x=h;
head.y=j;
end.x=e;
end.y=i+j;
}
}
if(s>0&&h!=0)
{
l=0;
e=e-x;
while(s>0&&e!=h-1)
{
s+=b[l];
l++;
e++;
if(s>sum)
{
sum=s;
head.x=h;
head.y=j;
end.x=e;
end.y=i+j;
}
}
}
}
}
System.out.print("最大子数组的和为:");
System.out.println(sum);
System.out.println("最大子数组为:");
if(end.x>head.x)
{
for(i=head.y;i<=end.y;i++)
{
for(j=head.x;j<end.x;j++)
{
System.out.print(a[i][j]);
System.out.print(" ");
}
System.out.println();
}
}
else
{
for(i=head.y;i<=end.y;i++)
{
for(j=head.x;j<x;j++)
{
System.out.print(a[i][j]);
System.out.print(" ");
}
for(j=0;j<end.x;j++)
{
System.out.print(a[i][j]);
System.out.print(" ");
}
System.out.println();
}
}
}
}
总结:
学会转换思路,讲一个大问题转换为几个小问题,慢慢的解决,一块一块的解决。
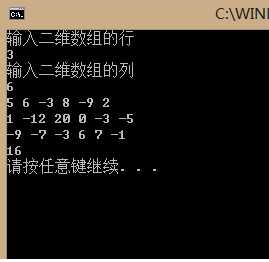
截图:
原文:http://www.cnblogs.com/dyc940210/p/4594429.html