Given a collection of numbers, return all possible permutations.
For example,[1,2,3] have the following permutations:[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], and [3,2,1].
本题题目很简单,关键是在于时间复杂度的考量。比较常规的方法是利用树的结构,然后递归实现。
下面描述利用树的结构递归求解的方法
考虑题目中给的数组,{1,2,3}(其实和数组无关,利用下标交织可以得到一个通用的方法,该方法的参数仅仅是数组长度N)。利用树的结构进行遍历交织,可以得到如下的结构:
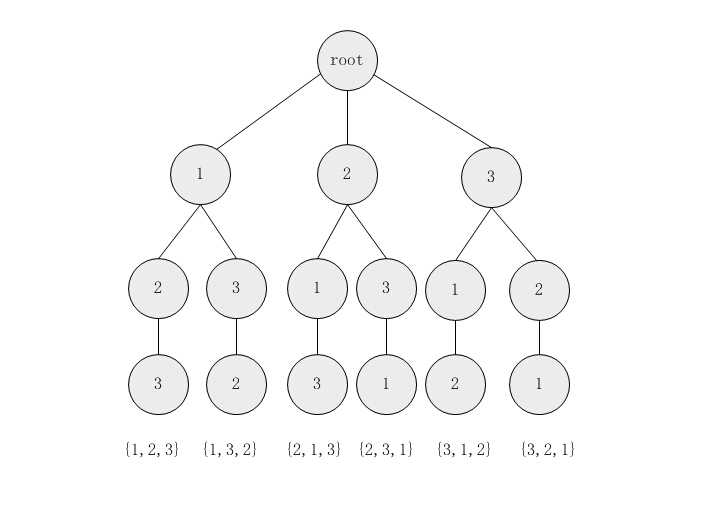
显然,在每一层,我们仅仅需要固定一个节点,到最后一层再向上返回就可以得到交织结果。
下面我们需要做的就是找到一个递归公式,以及终止递归条件即可。
现在假设原始数组长为N。
最开始的时候,我们固定一个元素(假设是第一个,顺序无关)此时另外N-1个元素需要交织。
现在就进入到了下一层,可以考虑这N-1个元素放在不同的框中的方法,即第一个框里面N-1个随便拿一个出来,剩下的N-2个元素可以放在下一层框子里面,以此类推。。。直到最后一层,返回。那么就得到了第一个交织结果。
但是我们现在需要输出所有交织的结果,那么在每一层中所固定的元素需要有一个遍历的操作,以第二层为例,第一次我们固定了编号为2的元素,那么下一次就要固定编号为3的,再下次就是编号为4的。。。直到遍历完所有的编号。
比较简单的方法就是每一次的第一个位置我们把它当作固定位置,每一次得到该位置的所有输出,就将其与下一个编号的元素交换,这样就保证了每一次遍历都有不同的数子作为固定数字,也就遍历的所有的交织。
void recursive(vector<int> nums){ for (int i=0;i<nums.size();i++){ swap(nums[0],nums[i]); doing recursive......; } }
完整代码如下:
class Solution { public: vector<vector<int>> permute(vector<int>& nums) { vector<vector<int>> ans; permute(ans, nums, 0); return ans; } void permute(vector<vector<int>>& ans, vector<int>& perm, int begin) { if (begin == perm.size()) { ans.push_back(perm); return; } for (int i=begin; i<perm.size(); i++) { if (i!=begin && perm[i] == perm[begin]) continue; swap(perm[i], perm[begin]); permute(ans, perm, begin+1); swap(perm[i], perm[begin]); } } };
值得说明的是:
1、i==begin时,即我们遍历的第一个元素就是固定元素,交换操作显得没什么意义。
2、perm[i] == perm[begin],表示当前的元素 perm[i] 以及固定元素 perm[begin]相等,即出现了重复的元素,如果替换过去向下递归,那么会得到和之前一样的输出,所以对于相同的元素,我们没必要计算(当然利用下标计算通用交织器时,这一点还需要做更多考量)
3、permute 夹在两个 swap之间,这是为了把之前交换的元素换回来,因为整个递归都是引用传递的perm参数,如果没有换回来的话,会产生一些重复输出,并且无法遍历到所有输出(简单思考一下,如果不换回来的话,数组尾部交织顺序打乱,当数组头部开始递归第二个编号的元素时,后面顺序是杂乱的)。
原文:http://www.cnblogs.com/ArcherCoder/p/4596368.html