Dijkstra算法
一.最短路径的最优子结构性质
该性质描述为:如果P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径,k和s是这条路径上的一个中间顶点,那么P(k,s)必定是从k到s的最短路径。下面证明该性质的正确性。
假设P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径,则有P(i,j)=P(i,k)+P(k,s)+P(s,j)。而 P(k,s)不是从k到s的最短距离,那么必定存在另一条从k到s的最短路径P‘(k,s),那么 P‘(i,j)=P(i,k)+P‘(k,s)+P(s,j)<P(i,j)。则与P(i,j)是从i到j的最短路径相矛盾。因此该性质得证。
二.Dijkstra算法
由上述性质可知,如果存在一条从i到j的最短路径(Vi.....Vk,Vj),Vk是Vj前面的一顶点。那么(Vi...Vk)也必定是从i到k的最短 路径。为了求出最短路径,Dijkstra就提出了以最短路径长度递增,逐次生成最短路径的算法。譬如对于源顶点V0,首先选择其直接相邻的顶点中长度最 短的顶点Vi,那么当前已知可得从V0到达Vj顶点的最短距离dist[j]=min{dist[j],dist[i]+matrix[i][j]}。根 据这种思路,
假设存在G=<V,E>,源顶点为V0,U={V0},dist[i]记录V0到i的最短距离,path[i]记录从V0到i路径上的i前面的一个顶点。
1.从V-U中选择使dist[i]值最小的顶点i,将i加入到U中;
2.更新与i直接相邻顶点的dist值。(dist[j]=min{dist[j],dist[i]+matrix[i][j]})
3.知道U=V,停止。
三.示例
先给出一个无向图
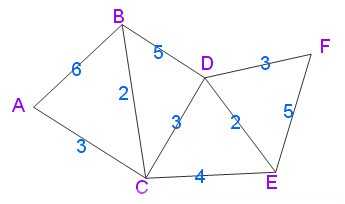
用Dijkstra算法找出以A为起点的单源最短路径步骤如下

代码:
#include <iostream> #include <stdio.h> #include <limits.h> using namespace std;
const int V = 9; //定义顶点个数 int prev[V];
//选取一个到S集合的最短距离的顶点。 int getMinIndex(int dist[V], bool sptSet[V]) { int min = INT_MAX, min_index; for (int v = 0; v < V; v++) if (visited[v] == false && dist[v] < min) min = dist[v], min_index = v; return min_index; } // 打印结果 void printPathDijkstra(int dist[], int n) { printf("Vertex Distance from Source\n"); for (int i = 0; i < V; i++) printf("%d \t\t %d\n", i, dist[i]); for (int i = 0; i < V; i++) { int path[V] = {0}; int step = 0; int cur = i; do
{ path[step++] = cur; cur = prev[cur]; } while (cur != -1);
for (int j = step - 1; j >= 0; j--) { printf("%d ", path[j]); } printf("\n"); } }
//source 代表源点 void dijkstra(int graph[V][V], int source) { int dist[V]; // 存储结果,从源点到 i的距离 bool visited[V]; // visited[i]=true 如果顶点i被访问过 // 初始化. 0代表不可达 #if 0 for (int i = 0; i < V; i++){ dist[i] = (graph[source][i] == 0 ? INT_MAX:graph[source][i]); visited[i] = false; } #endif
for (int i = 0; i < V; i++) { if(graph[source][i] == 0) { dist[i] = INT_MAX; prev[i] = -1; } else { dist[i] = graph[source][i]; prev[i] = source; } visited[i] = false; } // 源点,距离总是为0. 并加入SPT dist[source] = 0; visited[source] = true; // 迭代V-1次,因此不用计算源点了,还剩下V-1个需要计算的顶点。 for (int count = 0; count < V - 1; count++) { // u,是T集合中,到S集合距离最小的点 int u = getMinIndex(dist, sptSet); // 定点u设置为访问过 visited[u] = true; //更新到V的距离。可以理解为Bellman-Ford中的松弛操作 for (int v = 0; v < V; v++) if (!visited[v] && graph[u][v] && dist[u] != INT_MAX && dist[u] + graph[u][v] < dist[v]) { dist[v] = dist[u] + graph[u][v]; prev[v] = u; } } printPathDijkstra(dist, V); } int main() { /* 以例子中的图为例 */ int graph[V][V] = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 }, { 4, 0, 8, 0, 0, 0, 0, 11, 0 }, { 0, 8, 0, 7, 0, 4, 0, 0, 2 }, { 0, 0, 7, 0, 9, 14, 0, 0, 0 }, { 0, 0, 0, 9, 0, 10, 0, 0, 0 }, { 0, 0, 4, 0, 10, 0, 2, 0, 0 }, { 0, 0, 0, 14, 0, 2, 0, 1, 6 }, { 8, 11, 0, 0, 0, 0, 1, 0, 7 }, { 0, 0, 2, 0, 0, 0, 6, 7, 0 } }; dijkstra(graph, 0); return 0; }
另一种方法:

#include <stdio.h> #define MAX 6 #define MAX_VALUE 65536 typedef struct Node { int id; //节点id int distance; //到c1的距离 bool visited;//该点是否被访问 int parent; // 父节点 }Node; int v[MAX + 1][MAX + 1] = { 0 };//连接表 Node q[100]; //处理队列 int cur = 0; //尾指针 Node pts[MAX + 1];//标记每个点状态 void insert(Node it) { int i = 0; for (i = 0; i < cur; i++) { if (it.distance > q[i].distance) { break; } } for (int j = cur - 1; j >= i; j--) { q[j + 1] = q[j]; } q[i] = it; cur++; } void Dijkstra(int s) { for (int i = 1; i <= MAX; i++) { pts[i].id = i; pts[i].distance = MAX_VALUE; pts[i].visited = false; pts[i].parent = 0; } pts[s].distance = 0; q[cur++] = pts[s]; while (cur!=0) { cur--; Node c = q[cur]; if (pts[c.id].visited)continue; pts[c.id].visited = true; for (int i = 1; i <= MAX; i++) { if (i == c.id)continue; if (pts[i].visited)continue; if (v[c.id][i] == MAX_VALUE)continue; if (pts[i].distance > pts[c.id].distance + v[c.id][i]) { pts[i].distance = pts[c.id].distance + v[c.id][i]; pts[i].parent = c.id; insert(pts[i]); } } } } void initV(void) { for (int i = 1; i <= MAX; i++) for (int j = 1; j <= MAX; j++) { v[i][j] = MAX_VALUE; } } int a[10] = { 5, 3, 9, 8, 1, 2, 7, 6, 4, 0 }; void qsort(int begin, int end) { if (begin >= end)return; int left = begin; int right = end; int key = a[left]; while (left < right) { while ((left < right) && (a[right] <= key))right--; a[left] = a[right]; while ((left < right) && (a[left] >= key))left++; a[right] = a[left]; } a[left] = key; qsort(begin, left-1); qsort(left+1, end); } void printPathDijkstra() { for (int i = 1; i <= MAX; i++) { printf("%d %d\n", pts[i].id, pts[i].distance); } for (int i = 1; i <= MAX; i++) { int path[MAX] = {0}; int step = 0; int cur = i; do { path[step++] = cur; cur = pts[cur].parent; } while (cur != 0); for (int j = step - 1; j >= 0; j--) { printf("%d ", path[j]); } printf("\n"); } } int main(int argc, char** argv) { freopen("input.txt", "r", stdin); int N; scanf("%d\n", &N); qsort(0, 9); for (int case_num = 0; case_num < N; case_num++) { initV(); int line_num; scanf("%d\n", &line_num); for (int i = 0; i < line_num; i++) { int pt1, pt2, distance; scanf("%d %d %d", &pt1, &pt2, &distance); v[pt1][pt2] = distance; v[pt2][pt1] = distance; } Dijkstra(1); printPathDijkstra(); } }
输入用例:

1 10 1 2 4 1 3 8 2 3 3 2 4 4 2 5 6 3 4 2 3 5 2 4 5 4 4 6 9 5 6 4
Algorithm --> Dijkstra和Floyd最短路径算法
原文:http://www.cnblogs.com/jeakeven/p/4634397.html