快速排序,应用到分治法。
下面先了解一下什么是分治法?
分治法,顾名思义,分而治之。先将问题进行分解,然后将分离的问题进行求解,最后将所有分离的解进行合并,得到最终解。
分治法,“大事化小,小事化了,了后一合,大事得解”嗯哪,就是这样。。。。
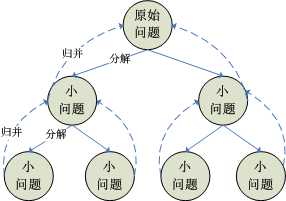
那么了解了分治法以后,再来解决问题,归并排序。(其实算法中有那么多排序一直搞不清楚,也分不清,他怎么就叫这个名字,虽然知道了名字,但是还是不知道是怎样解决问题的,怎么解决这个问题呢?这是费解。。。。。还没有想出来很好 的办法来记住。只好先死记硬背了)
好了废话不多说,进行分析求解。

SPARKS语言
procedure MERGESORT(low,high)
integer low,high;
if low<high
then mid<-(low+high)/2;//分割点
call MERGESORT(low,mid)//对前一部分进行排序
call MERGESORT(mid+1,high)//对后一部分进行排序
call MERGE(low,mid,high)//最后将已经排序好的进行合并。
endif
end MERGESORT
下面是合并的
procedure MERGE(low,mid,high)//合并就好像玩纸牌是一共两副牌已排序,然后将两副牌整合成一副牌的过程分别比较两副牌的大小,放在另外一个位置最后在倒回原来的位置。
integer l,h,j,low,mid,high
global A(low,high);local B(low,high)
l<-low;h<-low;j<-mid+1
while h<=mid and j<=high do
if A(h)<A(j) then B(i)<-A(h);h<-h+1
else B(i)<-A(j);j<-j+1
endif
i<-i+1;
repeat
if h>mid then for k<-j to high do //如果其中一副牌已经完了,那么另外剩余的拍之间放到一副牌理即可
B(i)<-A(k);i<-i+1
repeat
else for k<-h to mid do
B(i)<-A(k);i<-i+1
repeat
endif
for k<-low to high do//倒到原来的位置
A(k)<-B(i)
repeat
end MERGE
原文:http://www.cnblogs.com/ysugyl/p/4641646.html