边界填充

一、点在多边形内的测试

1.多边形

    N条边N个顶点构成一条闭合曲线v₀,v₁,......,v_n-1,v₀

2.乔丹曲线定理（Jordan Curve Theorem）

    一条简单闭合曲线将平面分为两部分：内和外

3.奇偶测试

    从点p向任一方向做射线，计算其与多边形的交点：奇则p在内部，偶则在外部

4. 缠绕数目测试

    链接测试点和边界，沿着边界移动，看缠绕了该点多少圈

二、多边形的光栅化

1.基本多边形光栅化算法

    基于奇偶性测试

    步骤：

        ①计算每条边和其所有扫描线的交点I(x,y)并把它们存至一个列表里

        ②用(x,y)对交点进行分类

        ③从列表中提取范围并设置范围内的像素

    问题：

        如果一个多边形的顶点落在扫描线上，是计0、1还是2个交点

    解决：

        将一条边看做半闭合区间，y小的那边做闭合，y大的那边做开放

        水平线不做考虑

    效率低

2.扫描线多边形算法

    增强扫描线和边的一致性

    使用边表（ET）和活动边表（AET）

    算法：

        ①假定多边形的顶点被扫描转换至整数坐标

        ②以y递增的方向进行扫描，每一条x轴的平行线都是一条扫描线

        ③对图形的边，有如下两种情况：

            i.边与扫描线平行，不参加求交点运算，在扫描转换的过程中直接填充

            ii.边与扫描线不平行，参加求交点运算

        ④扫描线可能与边界在顶点相交，又有两种情况：

            i.该顶点在局部取最值（如：√）

            ii.不取最值

            这里利用前边讲到的取半开半闭区间可以避免这个问题

    步骤：

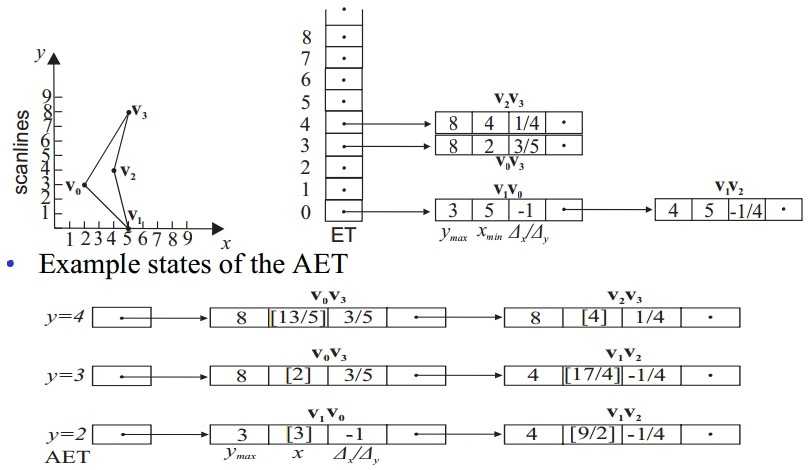
        ①建立一个边表（ET）

            在ET表示y_min，y=y_min时添加该边的记录。y_max为该边的y的最大值，x_min为y_min对应的x坐标值，然后有斜率的倒数以及指向下一条y=y_min的边

        ②以y递增进行扫描，当边的y_min等于当前扫描值时，将该边加入AET；当y_max≤y时，将该边从AET中移除

        ③对AET中的边进行求交，并进行两两配对，每一对表示多边形内部，进行填充

3.三角光栅化算法

     最简单的平面凸多边形光栅化算法（GL_POLYGON应该就是这样实现的吧）

     利用3条线的方程来判定一个点是不是在多边形内部：如果该点坐标带入3个方程所得结果的符号相同，则在同一个多边形内部（为什么呢？）

     算法：

triangle1 ( vertex v0, v1, v2, colour c )
{
    line l0, l1, l2;
    float e0, e1, e2, e0t, e1t, e2t;

    /* Compute the line coefficients (a,b,c) from the vertices */
    mkline(v0, v1, &l0); mkline(v1, v2, &l1); mkline(v2, v0, &l2);

    /* Compute bounding box of triangle */
    bb_xmin = min(v0.x, v1.x, v2.x); 
    bb_xmax = max(v0.x, v1.x, v2.x);
    bb_ymin = min(v0.y, v1.y, v2.y);
    bb_ymax = max(v0.y, v1.y, v2.y);

    /* Evaluate linear functions at (bb xmin, bb ymin) */
    e0 = l0.a * bb_xmin + l0.b * bb_ymin + l0.c;
    e1 = l1.a * bb_xmin + l1.b * bb_ymin + l1.c;
    e2 = l2.a * bb_xmin + l2.b * bb_ymin + l2.c;

    for(y=bb_ymin; y<=bb_ymax; y++)
    {
        e0t = e0; e1t = e1; e2t = e2;
        for(x=bb_xmin; x<=bb_xmax; x++)
        {
            if(sign(e0)==sign(e1)==sign(e2)) 
                setpixel(x,y,c);
            e0 = e0 + l0.a;
            e1 = e1 + l1.a;
            e2 = e2 + l2.a;
        }
    e0 = e0t + l0.b;
    e1 = e1t + l1.b;
    e2 = e2t + l2.b;
    }
}

边界填充,布布扣,bubuko.com

边界填充

原文：http://www.cnblogs.com/l00196472/p/3616775.html