题意:给出平面上N(<=100)个点,你需要找到一个这样的点,使得这个点到N个点的距离之和尽可能小。输出这个最小的距离和(四舍五入到最近的整数)
思路:三分求
三分算法解决凸形或者凹形函数的极值;
二分解决具有单调性的函数的极值;
如下图
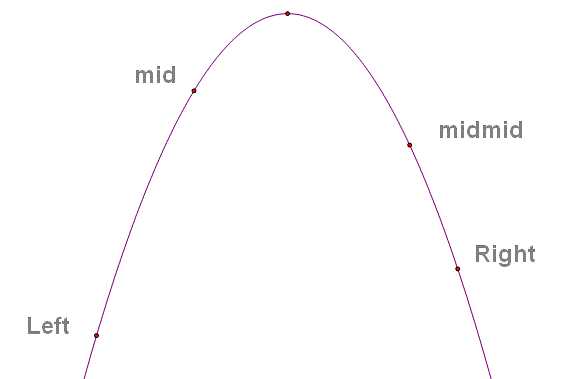
mid = (l+r) / 2;
midmid = (r+mid) / 2;
求极大值
if(cal(mid)>cal(midmid)) r= midmid;
else l = mid;
求极小值
if(cal(mid)<cal(midmid)) r= midmid;
else l = mid;/* **********************************************
Auther: xueaohui
Created Time: 2015-7-25 8:56:03
File Name : poj2420.cpp
*********************************************** */
#include <iostream>
#include <fstream>
#include <cstring>
#include <climits>
#include <deque>
#include <cmath>
#include <queue>
#include <stack>
#include <list>
#include <map>
#include <set>
#include <utility>
#include <sstream>
#include <complex>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <bitset>
#include <functional>
#include <algorithm>
using namespace std;
#define ll long long
#define N 111
int n;
struct node{
double x,y;
double dis(node a){
return sqrt((x-a.x)*(x-a.x)+(y-a.y)*(y-a.y));
}
}p[N];
double sum(double xx,double yy){
node a;
a.x = xx;
a.y = yy;
double d=0;
for(int i=1;i<=n;i++){
d+=a.dis(p[i]);
}
return d;
}
double cal(double xx){
double l = 0;
double r = 10000;
for(int i=1;i<=200;i++){
double mid = (l+r)/2;
double rmid = (mid+r)/2;
if(sum(xx,mid)<sum(xx,rmid)){
r = rmid;
}
else{
l = mid;
}
}
return sum(xx,l);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lf%lf",&p[i].x,&p[i].y);
}
double l = 0;
double r = 10000;
for(int i=1;i<=200;i++){
double mid = (l+r)/2;
double rmid = (mid+r)/2;
if(cal(mid)<cal(rmid)){
r = rmid;
}
else{
l = mid;
}
}
printf("%.0f\n",cal(l));
}
版权声明:都是兄弟,请随意转载,请注明兄弟是谁
原文:http://blog.csdn.net/u013076044/article/details/47053301