基于能量的模型(EBM)把我们所关心变量的各种组合和一个标量能量联系在一起。我们训练模型的过程就是不断改变标量能量的过程,因此就有了数学上期望的意义。比如,如果一个变量组合被认为是合理的,它同时也具有较小的能量。基于能量的概率模型通过能量函数来定义概率分布:
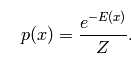 (1)
(1)
其中,正则化因子Z被称为配分函数:
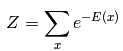
EBM可以通过对原始数据的负对数似然函数来运用梯度下降来完成训练。我们的过程也可以分为两步:1定义对数似然函数;2.定义损失函数。
对数似然函数:
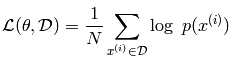
损失函数就是负对数似然函数:
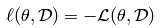
在许多情况下,我们无法观察到样品的所有参数;或者有时候为了提高系统的表达能力,我们希望引入一些不可见参数。因此我们把样品的所有参数分为两部分:可见的x部分和不可见的h部分。
在这种情况下,x的概率可以表达为边缘概率的方式:
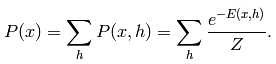
为了让形式上和式(1)统一,我们引入自由能量的概念:
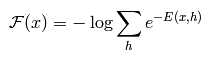
这样我们就可以把概率写为
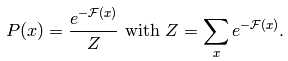
这样负对数似然函数梯度可以写成下面很有趣的形式:
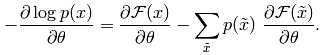
上面的梯度可以分为正负两部分,正的部分可以通过减小自由能量来增加训练数据的概率,而负的部分可以降低由模型生成的样品的可能性。
用解析的方法求梯度通常是非常困难的,因为需要计算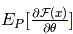 。
。
为了便于计算,我们要做的第一步是用确定数量的样品来进行估计,用来估计负梯度的样品叫做负粒子,梯度可以写成
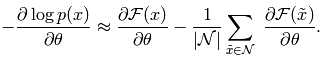
在这里我们理想的认为N中的x取样过程是满足概率P的。
通过上面的公式,整个运算过程基本上变的可行,唯一的问题是如何知道负粒子N,
受限玻尔兹曼机(RBM)
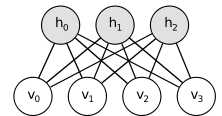
RBM的能量函数定义为:
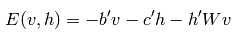
其中,W是连接权重,b和c分别是可见层和隐含层的偏置量。
自由能量公式就可以写为:
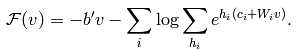
由于RBM元素之间的独立性:
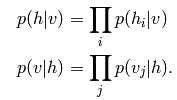
二进制的RBM
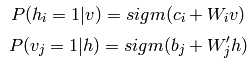
自由能量可以进一步简化为:
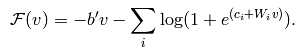
用二进制单元简化公式
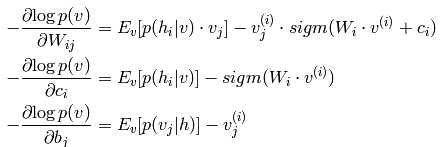
RBM中的取样
取样可通过收敛Markov chain完成,同时用Gibbs采样进行过渡操作。
对一个N个自由变量组成的样品进行Gibbs采样实际上通过计算每一个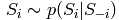 来完成。
来完成。
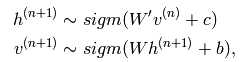
用图可以描述为
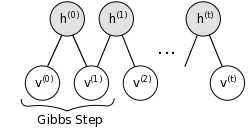
这个过程是相当耗时的。必须想办法提高效率。
CDK
CD采用两种技巧提高速度:
合适的初始化。
k步之后停止。通常k=1。
实现
RBM类的建立
class RBM(object): """Restricted Boltzmann Machine (RBM) """ def __init__(self, input=None, n_visible=784, n_hidden=500, W=None, hbias=None, vbias=None, numpy_rng=None, theano_rng=None): """ RBM constructor. Defines the parameters of the model along with basic operations for inferring hidden from visible (and vice-versa), as well as for performing CD updates. :param input: None for standalone RBMs or symbolic variable if RBM is part of a larger graph. :param n_visible: number of visible units :param n_hidden: number of hidden units :param W: None for standalone RBMs or symbolic variable pointing to a shared weight matrix in case RBM is part of a DBN network; in a DBN, the weights are shared between RBMs and layers of a MLP :param hbias: None for standalone RBMs or symbolic variable pointing to a shared hidden units bias vector in case RBM is part of a different network :param vbias: None for standalone RBMs or a symbolic variable pointing to a shared visible units bias """ self.n_visible = n_visible self.n_hidden = n_hidden if numpy_rng is None: # create a number generator numpy_rng = numpy.random.RandomState(1234) if theano_rng is None: theano_rng = RandomStreams(numpy_rng.randint(2 ** 30)) if W is None : # W is initialized with `initial_W` which is uniformely sampled # from -4.*sqrt(6./(n_visible+n_hidden)) and 4.*sqrt(6./(n_hidden+n_visible)) # the output of uniform if converted using asarray to dtype # theano.config.floatX so that the code is runable on GPU initial_W = numpy.asarray(numpy.random.uniform( low=-4 * numpy.sqrt(6. / (n_hidden + n_visible)), high=4 * numpy.sqrt(6. / (n_hidden + n_visible)), size=(n_visible, n_hidden)), dtype=theano.config.floatX) # theano shared variables for weights and biases W = theano.shared(value=initial_W, name=‘W‘) if hbias is None : # create shared variable for hidden units bias hbias = theano.shared(value=numpy.zeros(n_hidden, dtype=theano.config.floatX), name=‘hbias‘) if vbias is None : # create shared variable for visible units bias vbias = theano.shared(value =numpy.zeros(n_visible, dtype = theano.config.floatX),name=‘vbias‘) # initialize input layer for standalone RBM or layer0 of DBN self.input = input if input else T.dmatrix(‘input‘) self.W = W self.hbias = hbias self.vbias = vbias self.theano_rng = theano_rng # **** WARNING: It is not a good idea to put things in this list # other than shared variables created in this function. self.params = [self.W, self.hbias, self.vbias]
下一步是建立函数来完成(7)和(8)
def propup(self, vis): ‘‘‘ This function propagates the visible units activation upwards to the hidden units Note that we return also the pre_sigmoid_activation of the layer. As it will turn out later, due to how Theano deals with optimization and stability this symbolic variable will be needed to write down a more stable graph (see details in the reconstruction cost function) ‘‘‘ pre_sigmoid_activation = T.dot(vis, self.W) + self.hbias return [pre_sigmoid_activation, T.nnet.sigmoid(pre_sigmoid_activation)] def sample_h_given_v(self, v0_sample): ‘‘‘ This function infers state of hidden units given visible units ‘‘‘ # compute the activation of the hidden units given a sample of the visibles pre_sigmoid_h1, h1_mean = self.propup(v0_sample) # get a sample of the hiddens given their activation # Note that theano_rng.binomial returns a symbolic sample of dtype # int64 by default. If we want to keep our computations in floatX # for the GPU we need to specify to return the dtype floatX h1_sample = self.theano_rng.binomial(size=h1_mean.shape, n=1, p=h1_mean, dtype=theano.config.floatX) return [pre_sigmoid_h1, h1_mean, h1_sample] def propdown(self, hid): ‘‘‘This function propagates the hidden units activation downwards to the visible units Note that we return also the pre_sigmoid_activation of the layer. As it will turn out later, due to how Theano deals with optimization and stability this symbolic variable will be needed to write down a more stable graph (see details in the reconstruction cost function) ‘‘‘ pre_sigmoid_activation = T.dot(hid, self.W.T) + self.vbias return [pre_sigmoid_activation, T.nnet.sigmoid(pre_sigmoid_activation)] def sample_v_given_h(self, h0_sample): ‘‘‘ This function infers state of visible units given hidden units ‘‘‘ # compute the activation of the visible given the hidden sample pre_sigmoid_v1, v1_mean = self.propdown(h0_sample) # get a sample of the visible given their activation # Note that theano_rng.binomial returns a symbolic sample of dtype # int64 by default. If we want to keep our computations in floatX # for the GPU we need to specify to return the dtype floatX v1_sample = self.theano_rng.binomial(size=v1_mean.shape,n=1, p=v1_mean, dtype=theano.config.floatX) return [pre_sigmoid_v1, v1_mean, v1_sample]
原文:http://www.cnblogs.com/Iknowyou/p/3633073.html