思路如下:
给定一个含有n个元素的整型数组a,求a中所有元素的和。问题的难点在于如何使用递归上。如果使用递归,则需要考虑如何进行递归执行的开始以及终止条件,首先如果数组元素个数为0,那么和为0。同时,如果数组元素个数为n,那么先求出前n-1个元素之和,再加上a[n-1]即可。此时可以完成递归功能。总之,递归就是在某个函数的执行过程中首先判断它的终止条件参数,终止条件参数满足终止条件则执行完毕,终止条件参数不满足终止条件则调用它自身执行某项运算,比如这里求和就是执行加法。凡是递归一定都有一个参数作为终止条件,比如这里是数组中未加入求和队列的元素个数,初始为数组长度。因为终止条件参数的初始值为数组长度,所以从数组的最后一个元素作为求和队列的第一个元素开始,每递归一次就将数组中的一个元素划归到求和队列中,同时将终止条件参数减1,直到其未为0,标明所有元素都已加入求和队列,返回求和队列的值即可。可见递归至少有两个参数,终止条件参数以及递归对象。
代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 |
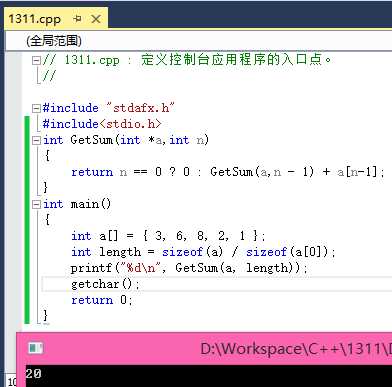
// 1311.cpp : 定义控制台应用程序的入口点。//#include "stdafx.h"#include<stdio.h>int GetSum(int
*a,int
n){ return
n == 0 ? 0 : GetSum(a,n - 1) + a[n-1];}int
main(){ int
a[] = { 3, 6, 8, 2, 1 }; int
length = sizeof(a) / sizeof(a[0]); printf("%d\n", GetSum(a, length)); getchar(); return
0;} |
效果如图:
原文:http://www.cnblogs.com/cysolo/p/3583661.html