| Time Limit: 8000MS | Memory Limit: 65536K | |
| Total Submissions: 6045 | Accepted: 1763 | |
| Case Time Limit: 2000MS | Special Judge |
Description
John is a Chief Executive Officer at a privately owned medium size company. The owner of the company has decided to make his son Scott a manager in the company. John fears that the owner will ultimately give CEO position to Scott if he does well on his new manager position, so he decided to make Scott’s life as hard as possible by carefully selecting the team he is going to manage in the company.
John knows which pairs of his people work poorly in the same team. John introduced a hardness factor of a team — it is a number of pairs of people from this team who work poorly in the same team divided by the total number of people in the team. The larger is the hardness factor, the harder is this team to manage. John wants to find a group of people in the company that are hardest to manage and make it Scott’s team. Please, help him.
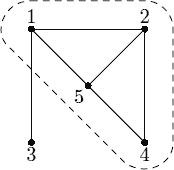
In the example on the picture the hardest team consists of people 1, 2, 4, and 5. Among 4 of them 5 pairs work poorly in the same team, thus hardness factor is equal to 5?4. If we add person number 3 to the team then hardness factor decreases to 6?5.
Input
The first line of the input file contains two integer numbers n and m (1 ≤ n ≤ 100, 0 ≤ m ≤ 1000). Here n is a total number of people in the company (people are numbered from 1 to n), and m is the number of pairs of people who work poorly in the same team. Next m lines describe those pairs with two integer numbers ai and bi (1 ≤ ai, bi ≤ n, ai ≠ bi) on a line. The order of people in a pair is arbitrary and no pair is listed twice.
Output
Write to the output file an integer number k (1 ≤ k ≤ n) — the number of people in the hardest team, followed by k lines listing people from this team in ascending order. If there are multiple teams with the same hardness factor then write any one.
Sample Input
sample input #1 5 6 1 5 5 4 4 2 2 5 1 2 3 1 sample input #2 4 0
Sample Output
sample output #1 4 1 2 4 5 sample output #2 1 1
Hint
Note, that in the last example any team has hardness factor of zero, and any non-empty list of people is a valid answer.
题意:给定一个无向图,选取一个密度最大的子图,就是边数/点数的比值最大,输出子图顶点,
一看这种题不大会,请教上交神牛:
设wi为子图边数,vi是子图点数,就是要max{wi-ans*vi}ans为二分的值,按边来考虑,如果选了一条边那么他连的两个端点都要被选,也就是
边也看做是点,点权为1,原来的点点权为-ans,求最大权闭合图就可以max这个值,然后类似最优比率生成树的二分下去(这是讲解)
代码:
/* ***********************************************
Author :rabbit
Created Time :2014/3/8 16:40:10
File Name :1718.cpp
************************************************ */
#pragma comment(linker, "/STACK:102400000,102400000")
#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <sstream>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#include <string>
#include <time.h>
#include <math.h>
#include <queue>
#include <stack>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define eps 1e-5
#define pi acos(-1.0)
typedef long long ll;
const int maxn=1110;
const int maxm=400010;
struct Edge{
int to,next;
double cap;
Edge(){};
Edge(int _next,int _to,double _cap){
next=_next;to=_to;cap=_cap;
}
}edge[maxm];
int head[maxn],tol,dep[maxn],cur[maxn],n,m;
void addedge(int u,int v,double flow){
edge[tol]=Edge(head[u],v,flow);head[u]=tol++;
edge[tol]=Edge(head[v],u,0);head[v]=tol++;
}
int Q[maxn];
bool bfs(int start,int end){
memset(dep,-1,sizeof(dep));
int front=0,rear=0;
dep[start]=0;Q[rear++]=start;
while(front!=rear){
int u=Q[front++];
for(int i=head[u];i!=-1;i=edge[i].next){
int v=edge[i].to;if(dep[v]==-1&&edge[i].cap>0){
Q[rear++]=v,dep[v]=dep[u]+1;
if(v==end)return 1;
}
}
}
return 0;
}
double dinic(int s,int t){
int i,top;double res=0;
int S[maxn],cur[maxn];
while(bfs(s,t)){
memcpy(cur,head,sizeof(head));
int u=s;top=0;
while(1){
if(u==t){
double min=INF;int loc;
for(int i=0;i<top;i++)if(min>edge[S[i]].cap)
min=edge[S[i]].cap,loc=i;
for(int i=0;i<top;i++)
edge[S[i]].cap-=min,edge[S[i]^1].cap+=min;
res+=min;top=loc;u=edge[S[top]^1].to;
}
for(int i=cur[u];i!=-1;cur[u]=i=edge[i].next)
if(edge[i].cap>0&&dep[u]+1==dep[edge[i].to])break;
if(cur[u]!=-1)S[top++]=cur[u],u=edge[cur[u]].to;
else{
if(top==0)break;
dep[u]=-1;u=edge[S[--top]^1].to;
}
}
}
return res;
}
int start[1111],end[1111];
double check(double mid){
memset(head,-1,sizeof(head));tol=0;
for(int i=1;i<=n;i++)addedge(i,n+m+1,mid);
for(int i=1;i<=m;i++){
addedge(0,n+i,1.0);
addedge(n+i,start[i],INF);
addedge(n+i,end[i],INF);
}
return m-dinic(0,n+m+1);
}
int fun(){
char ch;int flag=1,a=0;
while(ch=getchar())if((ch>=‘0‘&&ch<=‘9‘)||ch==‘-‘)break;
if(ch==‘-‘)flag=-1;else a=ch-‘0‘;
while(ch=getchar()){
if(ch>=‘0‘&&ch<=‘9‘)a=10*a+ch-‘0‘;
else break;
}
return flag*a;
}
int main(){
while(~scanf("%d%d",&n,&m)){
for(int i=1;i<=m;i++){
start[i]=fun();
end[i]=fun();
}
if(!m){
puts("1\n1");
continue;
}
double l=0,r=m;
while(r-l>eps){
double mid=(l+r)/2;
double ret=check(mid);
if(ret>0)l=mid;
else r=mid;
}
//cout<<"hahha: "<<l<<endl;
check(l);
//for(int i=1;i<=n;i++)cout<<dep[i]<<" ";cout<<endl;
int cnt=0;
//bfs(0,m+n+1);
for(int i=1;i<=n;i++)
if(dep[i]!=-1)cnt++;
printf("%d\n",cnt);
for(int i=1;i<=n;i++)
if(dep[i]!=-1)printf("%d\n",i);
}
return 0;
}
POJ 3155最大密度子图裸题,布布扣,bubuko.com
原文:http://blog.csdn.net/xianxingwuguan1/article/details/20795069